Question

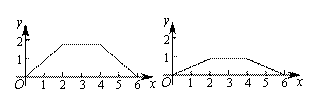
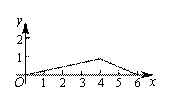
如图，菱形ABCD中，AB＝2，∠B＝120°，点M是AD的中点，点P由点A出发，沿A→B→C→D作匀速运动，到达点D停止，则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是

A B C D

Answer 1

A

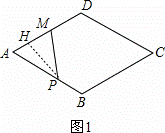
解：当点P在AB上运动时，即0≤x≤2，如图1，

作PH⊥AD于H，AP=x，

∵菱形ABCD中，AB=2，∠B=120°，点M是AD的中点，

∴∠A=60°，AM=2，

∴∠APH=30°，

在Rt△APH中，AH=AP=x，

PH=AH=x，

∴y=AM•PH=•2•x=x；

当点P在BC上运动时，即2＜x≤4，如图2，

作BE⊥AD于E，AP+BP=x，

∵四边形ABCD为菱形，∠B=120°，

∴∠A=60°，AM=2，AB=2，BC∥AD，

∴∠ABE=30°，

在Rt△ABE中，AE=AB=1，

PH=AE=，

∴y=AM•BE=•2•=；

当点P在CD上运动时，即4＜x≤6，如图3，

作PF⊥AD于F，AB+BC+PC=x，则PD=6﹣x，

∵菱形ABCD中，∠B=120°，

∴∠ADC=120°，

∴∠DPF=30°，

在Rt△DPF中，DF=DP=（6﹣x），

PF=DF=（6﹣x），

∴y=AM•PF=•2•（6﹣x）=（6﹣x）=﹣x+3，

∴△APM的面积y与点P经过的路程x之间的函数关系的图象为三段：当0≤x≤2，图象为线段，满足解析式y=x；当2≤x≤4，图象为平行于x轴的线段，且到x轴的距离为；当4≤x≤6，图象为线段，且满足解析式y=﹣x+3．