
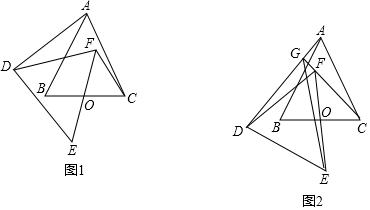
分析 (1)如图1中,结论:CF⊥AD,AD=$\sqrt{3}$CF;只要证明△ADO∽△COF,推出∠OAD=∠OCF,$\frac{CF}{AD}=\frac{OC}{AO}$=$\frac{\sqrt{3}}{3}$,由∠AKG=∠FKO,∠FCO+∠FKO=90°,
推出∠KAG+∠AKG=90°,即∠AGF90°,由此即可解决问题.
(2)如图2中,设DF的中点为M.连接EM、GM.因为点G在以DF为直径的圆上,当E、M、G共线时,EG=EM+MG的值最大,
解答 解:(1)如图1中,结论:CF⊥AD,AD=$\sqrt{3}$CF;
理由:连接AO、DO、延长CF交AD于G,如图1.
∵△ABC,△EFD均是边长为2的等边三角形,点D是边BC、EF的中点,
∴AO⊥BC,DO⊥EF,AO=DO,CO=OF,
∴∠AOD=90°-∠AOF=∠COF,$\frac{AO}{CO}$=$\frac{OD}{OF}$,
∴△ADO∽△COF,
∴∠OAD=∠OCF,$\frac{CF}{AD}=\frac{OC}{AO}$=$\frac{\sqrt{3}}{3}$,
∵∠AKG=∠FKO,∠FCO+∠FKO=90°,
∴∠KAG+∠AKG=90°,
∴∠AGF90°,
∴AD⊥CF,
∴CF⊥AD,AD=$\sqrt{3}$CF;
(2)如图2中,设DF的中点为M.连接EM、GM.
∵CF⊥AD,
∴∠DGF=90°,
∴点G在以DF为直径的圆上,
∵EG<EM+GM,
∴当E、M、G共线时,EG=EM+MG的值最大,
∵EM=DE•sin60°=$\sqrt{3}$,GM=$\frac{1}{2}$DF=1,
∴EG的最大值为$\sqrt{3}$+1.
点评 本题考查等边三角形的性质、旋转变换、相似三角形的判定和性质,直角三角形斜边中线的性质等知识,解题的关键是灵活运用相似三角形的性质解决问题,学会利用三角形三边关系解决最值问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
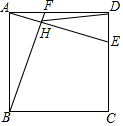 如图,在边长为2的正方形ABCD中,点E在边DC上运动,点F在边AD上运动,且DE=AF,AE,BF交于点H,连接DH,则DH的最小值为$\sqrt{5}-1$.
如图,在边长为2的正方形ABCD中,点E在边DC上运动,点F在边AD上运动,且DE=AF,AE,BF交于点H,连接DH,则DH的最小值为$\sqrt{5}-1$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com