
【题目】高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
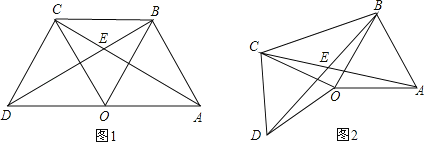
【题目】(1)如图1,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小;
(2)如图2,△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕点O旋转(△OAB和△OCD不能重叠),求∠AEB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求一次函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C在x轴上,且△ABC的面积是8,求此时点C的坐标;
(3)反比例函数y=![]() (1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)
(1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“最美女教师”张丽莉,为抢救两名学生,以致双腿高位截肢,社会各界纷纷为她捐款,我市某中学九年级一班全体同学参加了捐款活动,该班同学捐款情况的部分统计图如图所示:

(1)求该班的总人数;
(2)将条形图补充完整,并写出捐款总额的众数;
(3)该班平均每人捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铜仁某校高中一年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球,共投10次.甲、乙两名同学测试情况如图所示:

![]() 根据图6提供的信息填写下表:
根据图6提供的信息填写下表:
平均数 | 众数 | 方差 | |
甲 |
| ||
乙 |
|
![]() 如果你是高一学生会文体委员,会选择哪名同学进入篮球队?请说明理由.
如果你是高一学生会文体委员,会选择哪名同学进入篮球队?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级![]() 班同学小明和小亮,升入九年级时学校采用随机的方式编班,已知九年级共分六个班,小明和小亮被分在同一个班的概率是( )
班同学小明和小亮,升入九年级时学校采用随机的方式编班,已知九年级共分六个班,小明和小亮被分在同一个班的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC内一点D,点C是AE上一点,AD交BE于点P,射线DC交BE的延长线于点F,且∠ABD=∠ACD,∠PDB=∠PDC
(1)求证:AB=AC;
(2)若AB=3,AE=5,求![]() 的值;
的值;
(3)若![]() ,
,![]() =m,则
=m,则![]() =_______.
=_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.

(1)求证:AE=CF;
(2)求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边三角形
是等边三角形![]() 内一点,
内一点,![]() 将
将![]() 绕点
绕点![]() .按顺时针方向旋转
.按顺时针方向旋转![]() 得
得![]() , 连接
, 连接![]() .
.
(1)求证:![]() 是等边三角形;
是等边三角形;
(2)当![]() 时, 试判断
时, 试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com