
科学研究发现,空气含氧量y(克/立方米)与海拔高度x(米)之间近似地满足一次函数关系,经测量,在海拔高度为0米的地方,空气含氧量约为299克/立方米,在海拔高度为2000米的地方,空气含氧量约为235克/立方米.
(1)求出y与x的函数表达式;
(2)已知某山的海拔高度为1400米,请你求出该山山顶处的空气含氧量约为多少?
(1)y=﹣0.032x+299;
(2)该山山顶处的空气含氧量约为254.2克/立方米.
解析试题分析:(1)设y与x的函数表达式为y=kx+b(k≠0),然后把x=0时,y=299,x=2000时,y=235代入得到关于k、b的二元一次方程组,求出k、b的值,即可得解;
(2)把x=1400代入函数表达式进行计算即可得解.
试题解析:(1)设y与x的函数表达式为y=kx+b(k≠0),
∵x=0时,y=299,x=2000时,y=235,
∴ ,
,
解得 ,
,
∴y=﹣0.032x+299;
(2)当x=1400时,
y=﹣0.032x+299=﹣0.032×1400+299=254.2克/立方米.
答:该山山顶处的空气含氧量约为254.2克/立方米.
考点:一次函数的应用.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a、b、c分别满足-(a-4)2≥0,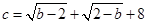
(1)求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标;
(2)直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,求 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系系xOy中,直线y=2x+m与y轴交于点A,与直线y=﹣x+4交于点B(3,n),P为直线y=﹣x+4上一点.
(1)求m,n的值;
(2)当线段AP最短时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知反比例函数y= 与一次函数y=kx+b的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与y轴的交点为C.
与一次函数y=kx+b的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与y轴的交点为C.
(1)求反比例函数和一次函数的解析式;
(2)若点D的坐标为(1,0),求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间为一次函数关系.根据图象提供的信息,解答下列问题:
(1)求出蜡烛燃烧时y与x之间的函数关系式;
(2)求蜡烛从点燃到燃尽所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,平面直角坐标系中,已知直线 上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转900至线段PD,过点D作直线AB⊥x轴。垂足为B,直线AB与直线
上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转900至线段PD,过点D作直线AB⊥x轴。垂足为B,直线AB与直线 交于点A,且BD=2AD,连接CD,直线CD与直线
交于点A,且BD=2AD,连接CD,直线CD与直线 交于点Q,则点Q的坐标为 。
交于点Q,则点Q的坐标为 。
查看答案和解析>>
科目:初中数学 来源: 题型:计算题
已知直线 与
与 轴交于点A(-4,0),与
轴交于点A(-4,0),与 轴交于点B.
轴交于点B.
【小题1】求b的值
【小题2】把△AOB绕原点O顺时针旋转90°后,点A落在 轴的
轴的 处,点B若在
处,点B若在 轴的
轴的 处;
处;
①求直线 的函数关系式;
的函数关系式;
②设直线AB与直线 交于点C,矩形PQMN是△
交于点C,矩形PQMN是△ 的内接矩形,其中点P,Q在线段
的内接矩形,其中点P,Q在线段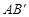 上,点M在线段
上,点M在线段 上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com