
分析 (1)先计算人数超过了50人,可以打折,实际总费用乘以0.9即可;
(2)由于人数不足50人,因此有两种购票方式,第一种按实际人数计算费有和,第二种按团体50人打折计算费用,分别计算并比较;
(3)先计算学生人数为x时购团体票比实际票便宜时的人数为x≥40$\frac{3}{5}$;因此根据此结果分三种情况计算:
①若41≤x≤46时,购团体最少;②若x>46时,按实际打折计算;③若0<x≤40时,按实际不打折计算.
解答 解:(1)因为总数不少于50人,根据题意得:
(4×30+15x)×0.9=108+13.5x,
答:该班买票至少应付(108+13.5x)元;
(2)若实际购票:因为42+4=46<50,则需费用为:42×15+4×30=750(元),
若购团体票,则需费用为:(4×30+46×15)×0.9=810×0.9=729(元),
∵750>729,
∴选择购50人团体票,最少付费729元;
(3)能,
4×30+15x≥(4×30+46×15)×0.9,
15x≥609,
x≥40$\frac{3}{5}$,
①若41≤x≤46时,最好团体购票,
则需费用:(4×30+46×15)×0.9=810×0.9=729(元),
②若x>46时,
则需费用为:(4×30+15x)×0.9=108+13.5x(元),
③若0<x≤40时,
则需费用:4×30+15x=120+15x(元),
答:若0<x≤40时,该班买票至少应付(120+15x)元;
若41≤x≤46时,该班买票至少应付729元;
若x>46时,该班买票至少应付(108+13.5x)元.
点评 本题考查了列代数式及代入求值问题,注意关键词语,前两问难度不大,第三问有难度,且容易出错,同时要注意第二问,要分情况进行计算.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
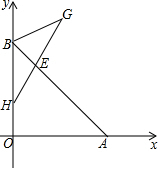 如图,点B(0,b),点A(a,0)分别在y轴、x轴正半轴上,且满足
如图,点B(0,b),点A(a,0)分别在y轴、x轴正半轴上,且满足查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲型号LED照明灯 | 乙型号LED照明灯 | |
| 进价(元/只) | 20 | 40 |
| 售价(元/只) | 30 | 55 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
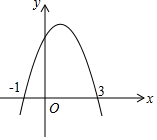 如图,抛物线y=ax2+bx+c交x轴于(-1,0)、(3,0)两点,以下四个结论正确的是(用序号表示)(1)(2)(3).
如图,抛物线y=ax2+bx+c交x轴于(-1,0)、(3,0)两点,以下四个结论正确的是(用序号表示)(1)(2)(3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com