
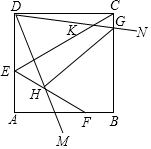
 正方形ABCD中,AB=4,点E为AD边上一点,点F为AB边上一点且∠DEC=∠AEF=60°,将顶点为D点的∠NDM绕着D点进行旋转,∠NDM=60°,若射线DM交线段EF于点H,若射线DN交线段EC于K点,交线段CB于G点,当HG平分∠DHF时,四边形EHGK的面积是$\frac{29}{15}\sqrt{3}$.
正方形ABCD中,AB=4,点E为AD边上一点,点F为AB边上一点且∠DEC=∠AEF=60°,将顶点为D点的∠NDM绕着D点进行旋转,∠NDM=60°,若射线DM交线段EF于点H,若射线DN交线段EC于K点,交线段CB于G点,当HG平分∠DHF时,四边形EHGK的面积是$\frac{29}{15}\sqrt{3}$. 分析 先延长CB,EF交于点P,过H作RQ⊥BC于Q,交AD于R,根据△PCE是等边三角形,推理可得△GHD≌△GHP,进而得到GP=GD,HP=HD,再设GP=GD=x,根据Rt△CDG中,($\frac{8}{3}\sqrt{3}$-x)2+42=x2,可得PG=$\frac{7}{3}\sqrt{3}$,CG=$\frac{\sqrt{3}}{3}$,即可得出S△CKG=$\frac{2}{15}\sqrt{3}$;设PH=DH=y,根据Rt△DRH中,($\frac{8}{3}\sqrt{3}$-$\frac{1}{2}$y)2+(4-$\frac{\sqrt{3}}{2}$y)2=y2,可得HP=$\frac{28}{15}\sqrt{3}$,HQ=$\frac{14}{5}$,进而得到S△PGH=$\frac{49}{15}\sqrt{3}$,最后根据S四边形EHGK=S△PCE-S△CKG-S△PGH进行计算即可.
解答 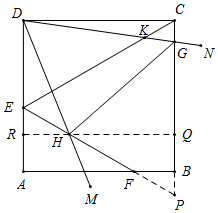 解:如图,延长CB,EF交于点P,过H作RQ⊥BC于Q,交AD于R,
解:如图,延长CB,EF交于点P,过H作RQ⊥BC于Q,交AD于R,
∵∠DEC=∠AEF=60°,AD∥BC,
∴∠CEP=∠P=∠PCE=60°,
∴△PCE是等边三角形,
∵AB=CD=4,
∴Rt△CDE中,CE=$\frac{8}{3}\sqrt{3}$=CP,DE=$\frac{4}{3}\sqrt{3}$,
∴AE=4-$\frac{4}{3}\sqrt{3}$,
∴Rt△AEF中,AF=4$\sqrt{3}$-4,
∴BF=8-4$\sqrt{3}$,
∴Rt△BPF中,BP=$\frac{8}{3}\sqrt{3}$-4,
∴CP=$\frac{8}{3}\sqrt{3}$-4+4=$\frac{8}{3}\sqrt{3}$,
当GH平分∠DHF时,∠GHD=∠GHP,
又∵∠GDH=∠P=60°,GH=GH,
∴△GHD≌△GHP,
∴GP=GD,HP=HD,
设GP=GD=x,则CG=CP-GP=$\frac{8}{3}\sqrt{3}$-x,
∴Rt△CDG中,($\frac{8}{3}\sqrt{3}$-x)2+42=x2,
解得x=$\frac{7}{3}\sqrt{3}$,
∴PG=$\frac{7}{3}\sqrt{3}$,CG=$\frac{\sqrt{3}}{3}$,$\frac{CG}{DE}=\frac{1}{4}$,
由CG∥DE,可得△CKG∽△EKD,
∴K到BC的距离为$\frac{1}{5}$×4=$\frac{4}{5}$,
∴S△CKG=$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$×$\frac{4}{5}$=$\frac{2}{15}\sqrt{3}$,
设PH=DH=y,则HQ=$\frac{\sqrt{3}}{2}$y,
∴RH=4-$\frac{\sqrt{3}}{2}$y,ER=$\frac{4}{3}\sqrt{3}$-$\frac{1}{2}$y,
∴DR=$\frac{8}{3}\sqrt{3}$-$\frac{1}{2}$y,
∵Rt△DRH中,($\frac{8}{3}\sqrt{3}$-$\frac{1}{2}$y)2+(4-$\frac{\sqrt{3}}{2}$y)2=y2,
解得y=$\frac{28}{15}\sqrt{3}$,
∴HP=$\frac{28}{15}\sqrt{3}$,HQ=$\frac{14}{5}$,
∴S△PGH=$\frac{1}{2}$×$\frac{7}{3}\sqrt{3}$×$\frac{14}{5}$=$\frac{49}{15}\sqrt{3}$,
∴S四边形EHGK=S△PCE-S△CKG-S△PGH
=$\frac{1}{2}$×$\frac{8}{3}\sqrt{3}$×4-$\frac{2}{15}\sqrt{3}$-$\frac{49}{15}\sqrt{3}$
=$\frac{29}{15}\sqrt{3}$.
故答案为:$\frac{29}{15}\sqrt{3}$.
点评 本题主要考查了正方形的性质,相似三角形的判定与性质以及旋转的性质的运用,解决问题的关键是作辅助线构造等边三角形以及全等三角形,依据直角三角形,运用勾股定理列方程求解.解题时注意方程思想的运用.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 018 | B. | 2 008 | C. | 2 014 | D. | 2 012 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )
如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )| A. | 9cm | B. | 12cm | C. | 15cm | D. | 18cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com