
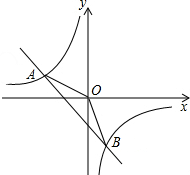
 如图所示,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-2,n),B(1,-3)两点.
如图所示,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-2,n),B(1,-3)两点.分析 (1)根据待定系数法,先求得反比例函数解析式,再求得一次函数解析式;
(2)利用坐标轴作为△AOB的分割线,求得△AOB的面积;
(3)在函数图象上观察,写出一次函数图象在反比例函数图象下方时所有的点的横坐标的集合.
解答 解:(1)∵一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-2,n),B(1,-3)两点
∴将B(1,-3)代入反比例函数y2=$\frac{m}{x}$可得
m=-3×1=-3
∴反比例函数为y2=$\frac{-3}{x}$
将A(-2,n)代入反比例函数为y2=$\frac{-3}{x}$可得
n=$\frac{3}{2}$,即A(-2,$\frac{3}{2}$)
将A(-2,$\frac{3}{2}$)、B(1,-3)代入一次函数y1=kx+b,可得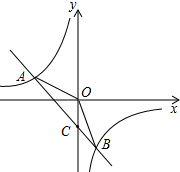
$\left\{\begin{array}{l}{-3=k+b}\\{\frac{3}{2}=-2k+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=-\frac{3}{2}}\end{array}\right.$
∴一次函数为y1=$-\frac{3}{2}$x-$\frac{3}{2}$
(2)如图,设一次函数图象与y轴交于点C,则
当x=0时,y=-$\frac{3}{2}$,即C(0,-$\frac{3}{2}$)
∴S△AOB=S△AOC+S△COB=$\frac{1}{2}$×$\frac{3}{2}$×2+$\frac{1}{2}$×$\frac{3}{2}$×1=$\frac{3}{2}$+$\frac{3}{4}$=$\frac{9}{4}$
(3)根据图象可得,使y1<y2的x的取值范围为:-2<x<0或x>1
点评 本题主要考查了反比例函数与一次函数的交点问题,需要掌握根据两个函数图象的交点坐标求两个函数解析式和有关不等式解集的方法.解答此类试题的依据是:①函数图象的交点坐标满足函数解析式;②不等式的解集就是其所对应的函数图象上满足条件的所有点的横坐标的集合.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
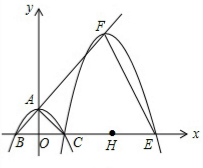 如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于点B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.
如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于点B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
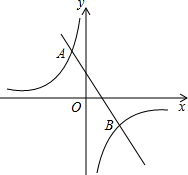 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$d的图象都经过点A(-2,6)和点B(4,n).
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$d的图象都经过点A(-2,6)和点B(4,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
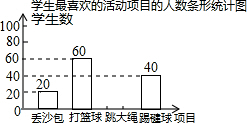 我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:| 项目 | 学生数(名) | 百分比 |
| 丢沙包 | 20 | 10% |
| 打篮球 | 60 | p% |
| 跳大绳 | n | 40% |
| 踢毽球 | 40 | 20% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com