
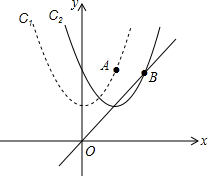
 如图,已知抛物线C1:y=$\frac{1}{2}$x2+2上有一点A,点A的横坐标为2.将抛物线C1向右平移,使其顶点落在直线y=x上,此时抛物线记作为C2,点A的对应点记作B.
如图,已知抛物线C1:y=$\frac{1}{2}$x2+2上有一点A,点A的横坐标为2.将抛物线C1向右平移,使其顶点落在直线y=x上,此时抛物线记作为C2,点A的对应点记作B.分析 (1)将A的点横坐标代入解析式求出纵坐标;由于抛物线C1对称轴就是y轴,故直接写出顶点坐标;根据平移法则写出抛物线C2的解析式;
(2)过点P作PN∥y轴交直线OB于点N,设出P点的横坐标,将△POB的面积用P点的横坐标表示,令面积等于8建立程,解出即可;
(3)设出Q点坐标,根据QM=QN,由两点间的距离公式列出等式,再结合抛物线C2的解析式,消去x,整理理成一个关于y和m的方程,而这个方程对任意的y都成立,从而确定m的取值.
解答 解:
(1)将A点横坐标代入抛物线C1:y=$\frac{1}{2}$x2+2可得y=4,
∴A(2,4),
抛物线C1:y=$\frac{1}{2}$x2+2顶点坐标为(0,2),
将抛物线C1:y=$\frac{1}{2}$x2+2向右平移两个单位得:$y=\frac{1}{2}(x-2)^{2}+2$=$\frac{1}{2}{x}^{2}-2x+4$;
(2)过点P作PN∥y轴交直线OB于点N,如图1,
A(2,4)向右平移两个单位得B(4,4),
∴B点也在直线y=x上,
设P(n,$\frac{1}{2}{n}^{2}-2n+4$),则N(n,n),
${S}_{△POB}=\frac{1}{2}×({x}_{B}-{x}_{O})×({y}_{P}-{y}_{N})$=n2-6n+8=8,
∴n(n-6)=0,
∴n=0或n=6,
∴P点坐标为(0,4)或(6,10);
(3)设Q(x,y),作QH垂直定直线于点N,如图2,
∵QM=QN,
∴(x-2)2+(y-m)2=(y-4+m)2,
∵$y=\frac{1}{2}{(x-2)}^{2}+2$,
∴(x-2)2=2y-4,
∴2y-4+(y-m)2=(y-4+m)2,
整理得:(2m-5)(y-1)=0,
上式对任意的y都成立,
∴m=$\frac{5}{2}$.
点评 本题考查了点与函数图象的关系、函数图象的平移、三角形面积的坐标表示(水平宽法)、两点间的距离公式,方程的恒成立问题等知识点,难度适中.第(2)当中用到的面积表示技巧极为重要,即三角形的面积等于水平宽与铅垂高乘积的二分之一,必须掌握;第(3)问实质上是抛物线的解析定义,定点即为抛物线的焦点,定直线即为抛物线的准线,这些概念同学们将在高中正式接触,在这里,对于初中而言,没必要知道这些概念,只需根据QM=QN建立方程即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
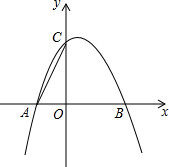 如图,二次函数y=-x2+bx+c的图象与x轴交于点A(-1,0),B(2,0),与y轴相交于点C.
如图,二次函数y=-x2+bx+c的图象与x轴交于点A(-1,0),B(2,0),与y轴相交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,Rt△ABC中,∠C=90°,D点和E点在AC,AB边上,且DE∥BC.P为线段DE上一点,使得∠CPB=90°,CP的延长线交AB于点M,延长AP交BC于点Q,过Q作PB的平行线交PC于点H,交AC于点S,T为BC延长线上一点,且满足$\frac{MP}{CP}•\frac{BT}{CT}$=$\frac{PE}{DP}$+$\frac{PM}{CH}$,连接TS.求证:TS⊥DQ.
如图,Rt△ABC中,∠C=90°,D点和E点在AC,AB边上,且DE∥BC.P为线段DE上一点,使得∠CPB=90°,CP的延长线交AB于点M,延长AP交BC于点Q,过Q作PB的平行线交PC于点H,交AC于点S,T为BC延长线上一点,且满足$\frac{MP}{CP}•\frac{BT}{CT}$=$\frac{PE}{DP}$+$\frac{PM}{CH}$,连接TS.求证:TS⊥DQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧,与y轴交于点C,点A、点B的横坐标是一元二次方程x2-4x-12=0的两个根.
已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧,与y轴交于点C,点A、点B的横坐标是一元二次方程x2-4x-12=0的两个根.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
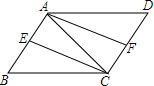 如图,已知在平行四边形ABCD中,AC=BC,E,F为AB和CD边的中点,
如图,已知在平行四边形ABCD中,AC=BC,E,F为AB和CD边的中点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 等腰△ABC中,腰长AB=8cm,BC=5cm,∠CBD=18°,AB的垂直平分线MN交AC于点D.
等腰△ABC中,腰长AB=8cm,BC=5cm,∠CBD=18°,AB的垂直平分线MN交AC于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com