
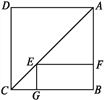
【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40 cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
【答案】(1)见解析;(2)20cm(3)当AF=5 cm时,四边形BFEG是正方形.
【解析】(1)由正方形的性质可得出AB⊥BC、∠B=90°,根据EF⊥AB、EG⊥BC利用“垂直于同一条直线的两直线互相平行”,即可得出EF∥GB、EG∥BF,再结合∠B=90°,即可证出四边形BFEG是矩形;
(2)由正方形的周长可求出正方形的边长,根据正方形的性质可得出△AEF为等腰直角三角形,进而可得出AF=EF,再根据矩形的周长公式即可求出结论;
(3)由正方形的判定可知:若要四边形BFEG是正方形,只需EF=BF,结合AF=EF、AB=10cm,即可得出结论.
(1)证明:∵四边形ABCD为正方形,
∴AB⊥BC,∠B=90°.
∵EF⊥AB,EG⊥BC,
∴EF∥GB,EG∥BF.
∵∠B=90°,
∴四边形BFEG是矩形;
(2)∵正方形ABCD的周长是40cm,
∴AB=![]() =10cm.
=10cm.
∵四边形ABCD为正方形,
∴△AEF为等腰直角三角形,
∴AF=EF,
∴四边形EFBG的周长C=2(EF+BF)=2(AF+BF)=20cm.
(3)若要四边形BFEG是正方形,只需EF=BF,
∵AF=EF,AB=10cm,
∴当AF=5cm时,四边形BFEG是正方形.


科目:初中数学 来源: 题型:
【题目】市煤气公司准备给某新建小区的用户安装管道煤气,现有![]() 用户提出了安装申请,此外每天还有新的用户提出申请,假设煤气公司每个安装小组安装的数量相同,且每天申请安装的用户数也相同,若煤气公司安排
用户提出了安装申请,此外每天还有新的用户提出申请,假设煤气公司每个安装小组安装的数量相同,且每天申请安装的用户数也相同,若煤气公司安排![]() 个安装小组同时做,则
个安装小组同时做,则![]() 天就可以装完所有新、旧用户的申请;若煤气公司安排
天就可以装完所有新、旧用户的申请;若煤气公司安排![]() 个安装小组同时做,则
个安装小组同时做,则![]() 天可以装完所有新旧用户的申请.
天可以装完所有新旧用户的申请.
![]() 求每天新申请安装的用户数及每个安装小组每天安装的数量;
求每天新申请安装的用户数及每个安装小组每天安装的数量;
![]() 如果要求在
如果要求在![]() 天内安装完所有新、旧用户的申请,但前
天内安装完所有新、旧用户的申请,但前![]() 天煤气公司只能派出
天煤气公司只能派出![]() 个安装小组安装,那么最后几天至少需要增加多少个安装小组同时安装,才能完成任务?
个安装小组安装,那么最后几天至少需要增加多少个安装小组同时安装,才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了统计知识后,数学老师请数学兴趣小组的同学就本班同学的上学方式进行了一次调查统计.如图甲乙是数学兴趣小组的同学们通过手机和整理数据后,绘制的两幅不完整的统计图.
请你根据图中提供的信息,解答一下的问题:
(1)在扇形统计图中,计算出“步行”部分所应对的圆心角的度数.
(2)请问该班共有多少名学生?
(3)在图中将表示“乘车”的部分补充完整.


查看答案和解析>>
科目:初中数学 来源: 题型:
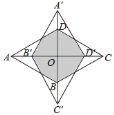
【题目】如图,菱形ABCD的一个内角是60,将它绕对角线的交点O顺时针旋转90后得到菱形A′B′C′D′.旋转前后两菱形重叠部分多边形的周长为![]() ,则菱形ABCD的边长为_________.
,则菱形ABCD的边长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试.计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,得到9分为优秀,成绩如表1所示,并制作了成绩分析表(表2).
表1
一班 | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
二班 | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
表2
班级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
一班 | 7.6 | 8 | 3.82 | 70% | 30% | |
二班 | b | 7.5 | 10 | 4.94 | 80% | 40% |
(1)在表2中,a= ,b= ;
(2)有人说二班的及格率、优秀率均高于一班,所以二班比一班好;但也有人认为一班成绩比二班好,请你给出坚持一班成绩好的两条理由;
(3)一班、二班获满分的中同学性别分别是1男1女、2男1女,现从这两班获满分的同学中各抽1名同学参加“汉字听写大赛”,用树状图或列表法求出恰好抽到1男1女两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
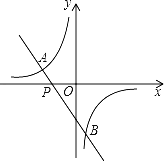
【题目】已知:如图,一次函数y=﹣2x﹣3的图象与反比例函数y=![]() (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.
(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用![]() 表示不大于
表示不大于![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() ,
,![]() ;用
;用![]() 表示大于
表示大于![]() 的最小整数,例如:
的最小整数,例如:![]() ,
,![]() ,
,![]() .解决下列问题:
.解决下列问题:
(1)![]() = ,,
= ,,![]() = ;
= ;
(2)若![]() =2,则
=2,则![]() 的取值范围是 ;若
的取值范围是 ;若![]() =-1,则
=-1,则![]() 的取值范围是 ;
的取值范围是 ;
(3)已知![]() ,
,![]() 满足方程组
满足方程组![]() ,求
,求![]() ,
,![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com