
【题目】综合题
(1)![]()
.
(2)解分式方程: ![]()
【答案】
(1)
解: ![]()
原式= ![]()
= ![]()
(2)
解:解分式方程: ![]()
去分母,得x-2(x-3)=4
去括号,得x-2x+6=4
移项,得x-2x=4-6
合并同类项,得-x=-2
解方程得x=2
经检验:x=2是原分式方程的根
解方程得x=2
经检验:x=2是原分式方程的根
【解析】(1)所有非零数的0次幂都等于1,sin45°=![]() ;去绝对值符号时,要注意负数的绝对值是它的相反数;
;去绝对值符号时,要注意负数的绝对值是它的相反数;
(2)解分式方程:去分母,去括号,移项,合并同类项,未知数系数化为1,检验方程的解.
【考点精析】通过灵活运用去分母法和特殊角的三角函数值,掌握先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊;分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”即可以解答此题.


科目:初中数学 来源: 题型:
【题目】已知∠AOB=120°,∠COD=60°,OE平分∠BOC
(1)如图1.当∠COD在∠AOB的内部时
①若∠AOC=39°40′,求∠DOE的度数;
②若∠AOC=α,求∠DOE的度数(用含α的代数式表示),
(2)如图2,当∠COD在∠AOB的外部时,(1)中∠AOC与∠DOE的数量关系还成立吗?若成立,请推导出∠AOC与∠DOE的度数之间的关系;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线AB上一点O为端点作射线OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD=![]() ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的两边BC,AB分别在平面直角坐标系的x轴、y轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知AC=3 ![]() ,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( )
,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
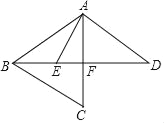
【题目】如图,已知AB=AC=AD,∠CAD=60°,分别连接BC、BD,作AE平分∠BAC交BD于点E,若BE=4,ED=8,则DF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+12x﹣30的顶点为A,对称轴AB与x轴交于点B.在x上方的抛物线上有C、D两点,它们关于AB对称,并且C点在对称轴的左侧,CB⊥DB.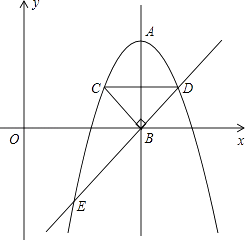
(1)求出此抛物线的对称轴和顶点A的坐标;
(2)在抛物线的对称轴上找出点Q,使它到A、C两点的距离相等,并求出点Q的坐标;
(3)延长DB交抛物线于点E,在抛物线上是否存在点P,使得△DEP的面积等于△DEC的面积?若存在,请你直接写出点P的坐标;若不存在,请说明理由.
提示:抛物线y=ax2+bx+c(a≠0)的对称轴为 ![]() ,顶点坐标为
,顶点坐标为 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com