
【题目】某同学在研究二次函数及其图像性质的问题时,发现了两个重要结论:
①抛物线 y = ax 2 2x + 3(a ≠0) ,不论 a 为何值时,它的顶点都在某条直线上;
②抛物线 y = ax 2 2x + 3(a ≠0),其顶点的横坐标减少![]() ,纵坐标增加
,纵坐标增加![]() 得到A点,若把顶点的横坐标增加
得到A点,若把顶点的横坐标增加![]() ,纵坐标增加
,纵坐标增加![]() ,得到B点,则A,B两点一定在抛物线y = ax 2 2x + 3上.
,得到B点,则A,B两点一定在抛物线y = ax 2 2x + 3上.
(1)请你帮忙求出抛物线 y = ax 2 2x + 3的顶点所在直线的解析式,并证明结论②是正确的;
(2)问题(1)中的直线上有一个点不是该抛物线的顶点,你能找出它来吗,并说明理由;
(3)你能把结论①或②(选择其中之一)推广到一般情况吗,请用数学语言表述你的成 果,并给予严格的证明.
【答案】(1)![]() ,证明见解析;(2)(0,3),理由见解析;(3)①的推广:若b、c是常数,对任意的实数
,证明见解析;(2)(0,3),理由见解析;(3)①的推广:若b、c是常数,对任意的实数![]() ,抛物线
,抛物线![]() 的顶点在直线
的顶点在直线![]() 上;②的推广:抛物线
上;②的推广:抛物线![]()
![]() ,将其顶点的横坐标增加或减少
,将其顶点的横坐标增加或减少![]() ,纵坐标增加
,纵坐标增加![]() ,所得到的两个点一定仍在抛物线上;证明见解析.
,所得到的两个点一定仍在抛物线上;证明见解析.
【解析】
(1)首先将抛物线y=ax2+2x+3转化成顶点式,写出用a表示的顶点坐标,消去a写出y关于x的表达式;
(2)观察(1)中的顶点坐标![]() ,因为
,因为![]() ,即横坐标
,即横坐标![]() ,纵坐标
,纵坐标![]() ,即可求得结果;
,即可求得结果;
(3)首先写出抛物线的一般形式,再转化成顶点式,将顶点的横坐标增加
代入一般式,验证纵坐标也增加.
解:(1)方法一:
当![]() 时,
时,![]() 的顶点坐标为(1,2),
的顶点坐标为(1,2),
当![]() 时,
时,![]() 的顶点坐标为(1,4),
的顶点坐标为(1,4),
设抛物线![]() 的顶点在直线
的顶点在直线![]() 上,
上,
将(1,2),(1,4)代入,得:
![]() ,解得:
,解得:![]() ,
,
所以![]() ,
,
即抛物线![]() 的顶点在直线
的顶点在直线![]() ;
;
方法二:
易知![]() 的顶点是
的顶点是![]() ,
,
即![]() ,
,![]() ,
,
消去a得:![]() ,
,
即抛物线![]() 的顶点在直线
的顶点在直线![]() ;
;
证明:抛物线![]() 的顶点是
的顶点是![]() ,
,
由题意得:A(0,3),B(![]() ,3),
,3),
当x=0时,y=3,则点A在抛物线![]() 上,
上,
当x=![]() 时,
时,![]() ,则点B抛物线
,则点B抛物线![]() 上,
上,
(2)直线![]() 上有一点(0,3)不是该抛物线的顶点,
上有一点(0,3)不是该抛物线的顶点,
抛物线![]() 的顶点是
的顶点是![]() ,
,
当![]() 时,横坐标
时,横坐标![]() ,即(0,3)不是抛物线的顶点;
,即(0,3)不是抛物线的顶点;
(3)①的推广
若b、c是常数,对任意的实数![]() ,抛物线
,抛物线![]() 的顶点在直线
的顶点在直线![]() 上.
上.
当![]() 时,则
时,则![]() 的顶点为
的顶点为![]() ,
,
当![]() 时,则
时,则![]() 的顶点为
的顶点为![]() ,
,
将它们代入![]() 得:
得:
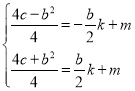 ,
,
解得:![]()
则直线为![]() ,
,
事实上,![]() 时,
时,
![]() ,
,
即抛物线顶点![]() 在直线
在直线![]() 上;
上;
②的推广
猜想:抛物线y = ax 2 2x + 3(a ≠0) ,将其顶点的横坐标增加或减少![]() ,纵坐标增加
,纵坐标增加![]() ,所得到的两个点一定仍在抛物线上.
,所得到的两个点一定仍在抛物线上.
证明:抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,
,
将其横坐标增加或减少![]() ,纵坐标增加
,纵坐标增加![]() ,得到
,得到
![]() ,
,![]()
将![]() 代入
代入![]() 得
得
![]()
=![]()
=![]()
∴点A在抛物线![]() 上,同理可证点B也在抛物线上.
上,同理可证点B也在抛物线上.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】在“双十一”购物街中,某儿童品牌玩具专卖店购进了![]() 两种玩具,其中
两种玩具,其中![]() 类玩具的金价比
类玩具的金价比![]() 玩具的进价每个多
玩具的进价每个多![]() 元.经调查发现:用
元.经调查发现:用![]() 元购进
元购进![]() 类玩具的数量与用
类玩具的数量与用![]() 元购进
元购进![]() 类玩具的数量相同.
类玩具的数量相同.
(1)求![]() 的进价分别是每个多少元?
的进价分别是每个多少元?
(2)该玩具店共购进![]() 了两类玩具共
了两类玩具共![]() 个,若玩具店将每个
个,若玩具店将每个![]() 类玩具定价为
类玩具定价为![]() 元出售,每个
元出售,每个![]() 类玩具定价
类玩具定价![]() 元出售,且全部售出后所获得的利润不少于
元出售,且全部售出后所获得的利润不少于![]() 元,则该淘宝专卖店至少购进
元,则该淘宝专卖店至少购进![]() 类玩具多少个?
类玩具多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】跳跳一家外出自驾游,出发时油箱里还剩有汽油30升,已知跳跳家的汽车每百千米的平均油耗为12升,设油箱里剩下的油量为y(单位:升),汽车行驶的路程为x(单位:千米).
(1)求y关于x的函数表达式;
(2)若跳跳家的汽车油箱中的油量低于5升时,仪表盘会亮起黄灯警报. 要使邮箱中的存油量不低于5升,跳跳爸爸至多能够行驶多少千米就要进加油站加油?
查看答案和解析>>
科目:初中数学 来源: 题型:
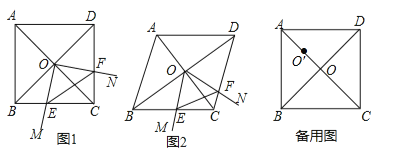
【题目】(12分)菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.
(1)如图1,当∠ABC=90°时,△OEF的形状是 ;
(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;
(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且![]() 时,直接写出线段CE的长.
时,直接写出线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 的图象与
的图象与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,且过点
,且过点![]() .
.
(1)求二次函数表达式;
(2)若点![]() 为抛物线上第一象限内的点,且
为抛物线上第一象限内的点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在抛物线上(![]() 下方)是否存在点
下方)是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 到
到![]() 轴的距离;若不存在,请说明理由.
轴的距离;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线![]() 经过直线
经过直线![]() 与坐标轴的两个交点
与坐标轴的两个交点![]() .此抛物线与
.此抛物线与![]() 轴的另一个交点为
轴的另一个交点为![]() .抛物线的顶点为
.抛物线的顶点为![]() .
.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 若点
若点![]() 为抛物线上一动点,是否存在点
为抛物线上一动点,是否存在点![]() .使
.使![]() 与
与![]() 的面积相等?若存在,求点
的面积相等?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市大力发展乡村旅游产业,全力打造客都美丽乡村”,其中“客家美景、客家文化、客家美食”享誉全省,游人络绎不绝.去年我市某村村民抓住机遇,投入20万元创办农家乐(餐饮+住宿),一年时间就收回投资的80%,其中餐饮收入是住宿收入的2倍还多1万元.
(1)求去年该农家乐餐饮和住宿的收入各为多少万元?
(2)今年该村村民再投入了10万元,增设了土特产的实体销售和网上销售项目并实现盈利,村民在接受记者采访时说,预计今年餐饮和住宿的收入比去年还会有10%的增长.这两年的总收入除去所有投资外还能获得不少于10万元的纯利润,请问今年土特产销售至少收入多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则图中阴影部分的面积是( )
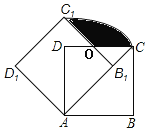
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com