
分析 根据勾股定理的逆定理得到△ABC是直角三角形,根据三角形的面积公式求出OA,根据翻折变换的性质解答即可.
解答 解: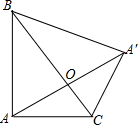 由翻折变换的性质可知,AA′⊥BC,OA=OA′,
由翻折变换的性质可知,AA′⊥BC,OA=OA′,
∵BC=10,AC=8,AB=6,
∴BC2=AC2+AB2,
∴△ABC是直角三角形,
∴$\frac{1}{2}$×AB×AC=$\frac{1}{2}$×BC×OA,即$\frac{1}{2}$×6×8=$\frac{1}{2}$×10×OA,
解得,OA=4.8,
∴AA′=9.6.
点评 本题考查的是翻折变换的性质,掌握翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,AB=AC,请你用两个与△ABC全等的三角形拼成一个四边形,并说明在你拼的图形中,其中一个三角形经过怎样的运动变化就可得到另一个三角形.
在△ABC中,AB=AC,请你用两个与△ABC全等的三角形拼成一个四边形,并说明在你拼的图形中,其中一个三角形经过怎样的运动变化就可得到另一个三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
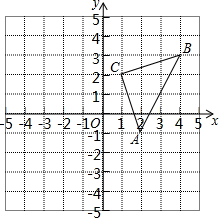 如图,平面直角坐标系中,△ABC的顶点都在网格点上,平移△ABC,使点B与坐标原点O重合,请在图中画出平移后的三角形A1OC1,并写出A1,C1的坐标.
如图,平面直角坐标系中,△ABC的顶点都在网格点上,平移△ABC,使点B与坐标原点O重合,请在图中画出平移后的三角形A1OC1,并写出A1,C1的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com