
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:填空题
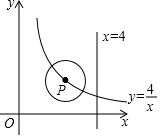 如图,P是双曲线y=$\frac{4}{x}$(x>0)的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与直线x=4相切时,点P的坐标为(3,$\frac{4}{3}$)或(5,$\frac{4}{5}$).
如图,P是双曲线y=$\frac{4}{x}$(x>0)的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与直线x=4相切时,点P的坐标为(3,$\frac{4}{3}$)或(5,$\frac{4}{5}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
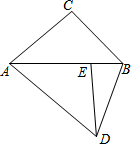 如图,将△ABC绕点A顺时针旋转,使点C落在边AB上的点E处,点B落在点D处,连结BD,如果∠DAC=∠DBA,那么∠BAC度数是36度.
如图,将△ABC绕点A顺时针旋转,使点C落在边AB上的点E处,点B落在点D处,连结BD,如果∠DAC=∠DBA,那么∠BAC度数是36度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知:四边形ABCD中,E为AB的中点,连接CE,DE,CD=CE=BE,DE∥BC.
如图,已知:四边形ABCD中,E为AB的中点,连接CE,DE,CD=CE=BE,DE∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
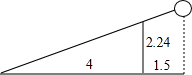 已知女排赛场标准球网的高度是2.24米,在2016年奥运会女排比赛中,某队球员在一次扣球时,球恰好擦网而过(击球擦网落地过程为直线),落在对方场地距离球网4米的位置上,此时该运动员距离球网1.5米,则该运动员击球的高度是3.08米.
已知女排赛场标准球网的高度是2.24米,在2016年奥运会女排比赛中,某队球员在一次扣球时,球恰好擦网而过(击球擦网落地过程为直线),落在对方场地距离球网4米的位置上,此时该运动员距离球网1.5米,则该运动员击球的高度是3.08米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
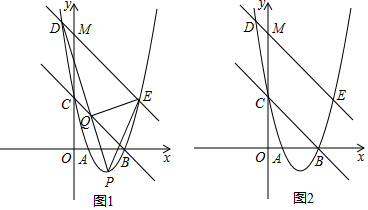
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com