
 如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC•
如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC•分析 (1)由AD∥BC,得到∠ADB=∠EBC,又因为∠A=∠CEB=90°,推出△ABD≌△ECB;
(2)根据等腰三角形的性质和直角三角形的性质得到结果;
(3)由全等三角形的性质得到对应边相等,利用勾股定理解出结果.
解答 解:(1)证明:∵AD∥BC,
∴∠ADB=∠EBC,
∵∠A=∠CEB=90°,
在△ABD与△CEB中,$\left\{\begin{array}{l}{∠A=∠CEB}\\{∠ADB=∠EBC}\\{AB=CE}\end{array}\right.$,
∴△ABD≌△ECB;
(2)由(1)证得△ABD≌△ECB,
∴BD=BC,
∴∠BCD=∠BDC=65°,
∵∠DCE=90°-65°=25°,
∴∠ECB=40°;
(3)由(1)证得△ABD≌△ECB,
∴CE=AB=4,BE=AB=3,
∴BD=BC=$\sqrt{{4}^{2}{+3}^{2}}$=5,
∴DE=2,
∴CD=$\sqrt{{2}^{2}{+4}^{2}}$=2$\sqrt{5}$.
点评 本题考查了全等三角形的性质,直角三角形的性质,等腰三角形的判定与性质,知识的综合运用是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 下列条件中,能说明AD∥BC的条件有( )个
下列条件中,能说明AD∥BC的条件有( )个| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,为了测量合浦文昌塔的高度,某校兴趣小组在塔前的平地A处安装了测角仪,测得塔顶的仰角∠α=30°,又沿着塔的方向前进25米到达B处测量,测得塔顶的仰角∠β=45°,已知测角仪的高AC=1.5米,请你根据上述数据,计算塔FG的高度(结果精确到0.1米).
如图,为了测量合浦文昌塔的高度,某校兴趣小组在塔前的平地A处安装了测角仪,测得塔顶的仰角∠α=30°,又沿着塔的方向前进25米到达B处测量,测得塔顶的仰角∠β=45°,已知测角仪的高AC=1.5米,请你根据上述数据,计算塔FG的高度(结果精确到0.1米).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
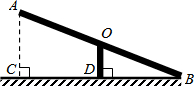 如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为100cm.
如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为100cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
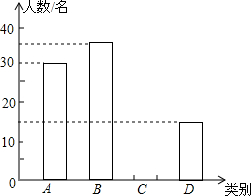 由于各地雾霾天气越来越严重,2015年春节前夕,蚌埠市某校团委向全校3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:不会减少烟花爆竹数量;D类:使用电子鞭炮”四个选项对100名学生进行问卷调查,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
由于各地雾霾天气越来越严重,2015年春节前夕,蚌埠市某校团委向全校3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:不会减少烟花爆竹数量;D类:使用电子鞭炮”四个选项对100名学生进行问卷调查,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:| 类别 | 频数 | 频率 |
| A | a | m |
| B | 35 | 0.35 |
| C | 20 | 0.20 |
| D | b | n |
| 合计 | 100 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )
如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com