
【题目】如图1,抛物线y=x2﹣2x+k与x轴交于A、B两点,与y轴交于点C(0,﹣3).[图2、图3为解答备用图]
(1)k= , 点A的坐标为 , 点B的坐标为;
(2)设抛物线y=x2﹣2x+k的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
(4)在抛物线y=x2﹣2x+k上求点Q,使△BCQ是以BC为直角边的直角三角形.
【答案】
(1)-3;(﹣1,0);(3,0)
(2)
解:∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的顶点为M(1,﹣4),连接OM.
则△AOC的面积= ![]() ,△MOC的面积=
,△MOC的面积= ![]() ,
,
△MOB的面积=6,
∴四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积=9.
说明:也可过点M作抛物线的对称轴,将四边形ABMC的面
积转化为求1个梯形与2个直角三角形面积的和
(3)
解:如图(2),设D(m,m2﹣2m﹣3),连接OD.
则0<m<3,m2﹣2m﹣3<0
且△AOC的面积= ![]() ,△DOC的面积=
,△DOC的面积= ![]() m,
m,
△DOB的面积=﹣ ![]() (m2﹣2m﹣3),
(m2﹣2m﹣3),
∴四边形ABDC的面积=△AOC的面积+△DOC的面积+△DOB的面积
=﹣ ![]() m2+
m2+ ![]() m+6
m+6
=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() .
.
∴存在点D( ![]() ,
, ![]() ),使四边形ABDC的面积最大为
),使四边形ABDC的面积最大为 ![]()

(4)
解:有两种情况:
如图(3),过点B作BQ1⊥BC,交抛物线于点Q1、交y轴于点E,连接Q1C.
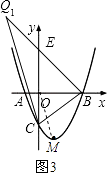
∵∠CBO=45°,
∴∠EBO=45°,BO=OE=3.
∴点E的坐标为(0,3).
∴直线BE的解析式为y=﹣x+3.
由 ![]()
解得 ![]()
∴点Q1的坐标为(﹣2,5).
如图(4),过点C作CF⊥CB,交抛物线于点Q2、交x轴于点F,连接BQ2.
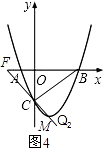
∵∠CBO=45°,
∴∠CFB=45°,OF=OC=3.
∴点F的坐标为(﹣3,0).
∴直线CF的解析式为y=﹣x﹣3.
由 ![]()
解得 ![]()
![]()
∴点Q2的坐标为(1,﹣4).
综上,在抛物线上存在点Q1(﹣2,5)、Q2(1,﹣4),使△BCQ1、△BCQ2是以BC为直角边的直角三角形.
说明:如图(4),点Q2即抛物线顶点M,直接证明△BCM为直角三角形同样可以.
【解析】解:(1)把C(0,﹣3)代入抛物线解析式y=x2﹣2x+k中得k=﹣3
∴y=x2﹣2x﹣3,
令y=0,
即x2﹣2x﹣3=0,
解得x1=﹣1,x2=3.
∴A(﹣1,0),B(3,0).
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠C为直角,AC=5,BC=12,在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放个. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;② ![]() ;③ac﹣b+1=0;④OAOB=﹣
;③ac﹣b+1=0;④OAOB=﹣ ![]() .其中正确结论的序号是 .
.其中正确结论的序号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y1=﹣x+4的图象与函数y2= ![]() (x>0)的图象交于A(m,1),B(1,n)两点.
(x>0)的图象交于A(m,1),B(1,n)两点. 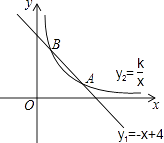
(1)求k,m,n的值;
(2)利用图象写出当x≥1时,y1和y2的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=x2﹣2x+k与x轴交于A、B两点,与y轴交于点C(0,﹣3).[图2、图3为解答备用图]
(1)k= , 点A的坐标为 , 点B的坐标为;
(2)设抛物线y=x2﹣2x+k的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
(4)在抛物线y=x2﹣2x+k上求点Q,使△BCQ是以BC为直角边的直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第一次模拟试后,数学科陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到右第二、三、四组的频数比为3:9:8,然后布置学生(也请你一起)结合统计图完成下列问题: 
(1)全班学生是多少人?
(2)成绩不少于90分为优秀,那么全班成绩的优秀率是多少?
(3)若不少于100分可以得到A+等级,则小明得到A+的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y= ![]() 和y=
和y= ![]() 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
① ![]() =
= ![]() ;
;
②阴影部分面积是 ![]() (k1+k2);
(k1+k2);
③当∠AOC=90°时,|k1|=|k2|;
④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.
其中正确的结论是(把所有正确的结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角△ABC中,∠C=90°,∠A、∠B与∠C的对边分别是a、b和c,那么下列关系中,正确的是( )
A.cosA= ![]()
B.tanA= ![]()
C.sinA= ![]()
D.cosA= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】立定跳远是小刚同学体育中考的选考项目之一.某次体育课上,体育老师记录了小刚的一组立定跳远训练成绩如下表:
成绩(m) | 2.35 | 2.4 | 2.45 | 2.5 | 2.55 |
次数 | 1 | 1 | 2 | 5 | 1 |
则下列关于这组数据的说法中正确的是( )
A.众数是2.45
B.平均数是2.45
C.中位数是2.5
D.方差是0.48
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com