
 如图,在菱形ABCD中,∠B=60°,AB=2,扇形AEF的半径为2,圆心角为60°,则阴影部分的面积是$\frac{2}{3}π$-$\sqrt{3}$.
如图,在菱形ABCD中,∠B=60°,AB=2,扇形AEF的半径为2,圆心角为60°,则阴影部分的面积是$\frac{2}{3}π$-$\sqrt{3}$. 分析 根据菱形的性质得出△ADC和△ABC是等边三角形,进而利用全等三角形的判定得出△ADH≌△ACG,得出四边形AGCH的面积等于△ADC的面积,进而求出即可.
解答  解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴∠B=∠D=60°,AB=AD=DC=BC=2,
∴∠BCD=∠DAB=120°,
∴∠1=∠2=60°,
∴△ABC、△ADC都是等边三角形,
∴AC=AD=2,
∵AB=2,
∴△ADC的高为$\sqrt{3}$,AC=2,
∵扇形BEF的半径为1,圆心角为60°,
∴∠4+∠5=60°,∠3+∠5=60°,
∴∠3=∠4,
设AF、DC相交于HG,设BC、AE相交于点G,
在△ADH和△ACG中,
$\left\{\begin{array}{l}{∠3=∠4}\\{AC=AD}\\{∠D=∠1=60°}\end{array}\right.$,
∴△ADH≌△ACG(ASA),
∴四边形AGCH的面积等于△ADC的面积,
∴图中阴影部分的面积是:S扇形AEF-S△ACD=$\frac{60•π×{2}^{2}}{360}$-$\frac{1}{2}$×2×$\sqrt{3}$=$\frac{2}{3}π$-$\sqrt{3}$,
故答案为:$\frac{2}{3}π$-$\sqrt{3}$.
点评 此题主要考查了扇形的面积计算以及全等三角形的判定与性质等知识,根据已知得出四边形EBFD的面积等于△ABD的面积是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
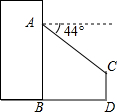 如图,李明在自家楼房的窗口A处,测量楼前的路灯CD的高度,现测得窗口处A到路灯顶部C的仰角为44°,到地面的距离AB为20米,楼底到路灯的距离BD为12米,求路灯CD的高度(结果精确到0.1)
如图,李明在自家楼房的窗口A处,测量楼前的路灯CD的高度,现测得窗口处A到路灯顶部C的仰角为44°,到地面的距离AB为20米,楼底到路灯的距离BD为12米,求路灯CD的高度(结果精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
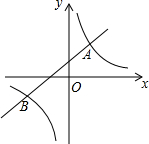 如图,直线y=kx+b(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)相交于A(1,2),B(n,-1)两点.
如图,直线y=kx+b(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)相交于A(1,2),B(n,-1)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.
在平面直角坐标xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 3 | 4 | 3 | 0 | -5 | … |
| A. | x1=2,x2=-2 | B. | x1=2,x2=-3 | C. | x1=2,x2=-4 | D. | x1=2,x2=-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com