
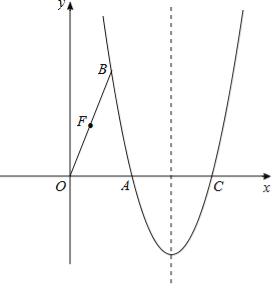
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() ОЙ§ЕуAЃЈ
ОЙ§ЕуAЃЈ![]() ЃЌ0ЃЉКЭЕуBЃЈ1ЃЌ
ЃЌ0ЃЉКЭЕуBЃЈ1ЃЌ![]() ЃЉЃЌгыxжсЕФСэвЛИіНЛЕуЮЊCЃЎ
ЃЉЃЌгыxжсЕФСэвЛИіНЛЕуЮЊCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЕуDдкЖдГЦжсЕФгвВрЃЌxжсЩЯЗНЕФХзЮяЯпЩЯЃЌЧвЁЯBDA=ЁЯDACЃЌЧѓЕуDЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНгBDЃЌНЛХзЮяЯпЖдГЦжсгкЕуEЃЌСЌНгAEЃЎ
ЂйХаЖЯЫФБпаЮOAEBЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЂкЕуFЪЧOBЕФжаЕуЃЌЕуMЪЧжБЯпBDЕФвЛИіЖЏЕуЃЌЧвЕуMгыЕуBВЛжиКЯЃЌЕБЁЯBMF=![]() ЁЯMFOЪБЃЌЧыжБНгаДГіЯпЖЮBMЕФГЄЃЎ
ЁЯMFOЪБЃЌЧыжБНгаДГіЯпЖЮBMЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЎЃЈ2ЃЉDЃЈ4ЃЌ
ЃЎЃЈ2ЃЉDЃЈ4ЃЌ![]() ЃЉЃЎЃЈ3ЃЉЂйЫФБпаЮOAEBЪЧЦНааЫФБпаЮЃЎРэгЩШчМћНтЮіЃЛЂкЯпЖЮBMЕФГЄЮЊ
ЃЉЃЎЃЈ3ЃЉЂйЫФБпаЮOAEBЪЧЦНааЫФБпаЮЃЎРэгЩШчМћНтЮіЃЛЂкЯпЖЮBMЕФГЄЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉНЋAЃЈ![]() ЃЌ0ЃЉКЭBЃЈ1ЃЌ
ЃЌ0ЃЉКЭBЃЈ1ЃЌ![]() ЃЉДњШыХзЮяЯпНтЮіЪН
ЃЉДњШыХзЮяЯпНтЮіЪН![]() ЃЌЕУЃК
ЃЌЕУЃК
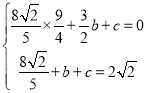 ЃЌНтЕУЃК
ЃЌНтЕУЃК ЃЌ
ЃЌ
НтЮіЪНЮЊЃК![]()
ЃЈ2ЃЉЕБЁЯBDA=ЁЯDACЪБЃЌBDЁЮxжсЃЌ
ЁпBЃЈ1ЃЌ![]() ЃЉЃЌЕБy=
ЃЉЃЌЕБy=![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
НтЕУЃКx=1Лђx=4ЃЌ
ЁрDЃЈ4ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЃЈ3ЃЉЂйЫФБпаЮOAEBЪЧЦНааЫФБпаЮ
РэгЩШчЯТЃКХзЮяЯпЕФЖдГЦжсЪЧ![]() ЃЌ
ЃЌ
ЁрBE=![]() -1=
-1=![]() ЃЌ
ЃЌ
ЁпAЃЈ![]() ЃЌ0ЃЉ
ЃЌ0ЃЉ
ЁрOA-BE=![]()
ЁпBEЁЮOA
ЁрЫФБпаЮOAEBЪЧЦНааЫФБпаЮ
ЂкЁпOЃЈ0ЃЌ0ЃЉЃЌBЃЈ1ЃЌ![]() ЃЉЃЌFЮЊOBЕФжаЕуЃЌ
ЃЉЃЌFЮЊOBЕФжаЕуЃЌ
ЁрFЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
Й§ЕуFзїFNЁЭжБЯпBDгкЕуNЃЌдђFN=![]() Љ
Љ![]() =
=![]() ЃЌBN=1Љ
ЃЌBN=1Љ![]() =
=![]() ЃЎ
ЃЎ
дкRtЁїBNFжаЃЌгЩЙДЙЩЖЈРэЕУЃК![]() ЃЎ
ЃЎ
ЁпЁЯBMF=![]() ЁЯMFOЃЌЁЯMFO=ЁЯFBM+ЁЯBMFЃЌ
ЁЯMFOЃЌЁЯMFO=ЁЯFBM+ЁЯBMFЃЌ
ЁрЁЯFBM=2ЁЯBMFЃЎ
ЃЈIЃЉЕБЕуMЮЛгкЕуBгвВрЪБЃЎ
дкжБЯпBDЩЯЕуBзѓВрШЁвЛЕуGЃЌЪЙBG=BF=![]() ЃЌСЌНгFGЃЌдђGN=BGЉBN=1ЃЌ
ЃЌСЌНгFGЃЌдђGN=BGЉBN=1ЃЌ
дкRtЁїFNGжаЃЌгЩЙДЙЩЖЈРэЕУЃК![]() ЃЎ
ЃЎ
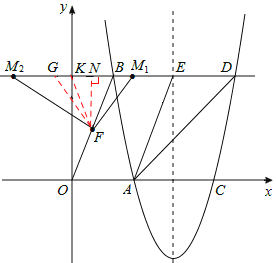
ЁпBG=BFЃЌ
ЁрЁЯBGF=ЁЯBFGЃЎ
гжЁпЁЯFBM=ЁЯBGF+ЁЯBFG=2ЁЯBMFЃЌ
ЁрЁЯBFG=ЁЯBMFЃЎ
гжЁпЁЯMGF=ЁЯMGFЃЌ
ЁрЁїGFBЁзЁїGMFЃЎ
Ёр![]() ЃЌМД
ЃЌМД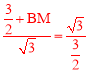 ЃЎ
ЃЎ
ЁрBM=![]() ЃЎ
ЃЎ
ЃЈIIЃЉЕБЕуMЮЛгкЕуBзѓВрЪБЃЌ
ЩшBDгыyжсНЛгкЕуKЃЌСЌНгFKЃЌдђFKЮЊRtЁїKOBаББпЩЯЕФжаЯпЃЌ
ЁрKF=![]() OB=FB=
OB=FB=![]() ЃЎ
ЃЎ
ЁрЁЯFKB=ЁЯFBM=2ЁЯBMFЃЎ
гжЁпЁЯFKB=ЁЯBMF+ЁЯMFKЃЌ
ЁрЁЯBMF=ЁЯMFKЃЎЁрMK=KF=![]() ЃЎ
ЃЎ
ЁрBM=MK+BK=![]() +1=
+1=![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌЯпЖЮBMЕФГЄЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ


 вЛХЕЪщвЕЪюМйзївЕПьРжМйЦкдЦФЯУРЪѕГіАцЩчЯЕСаД№АИ
вЛХЕЪщвЕЪюМйзївЕПьРжМйЦкдЦФЯУРЪѕГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌжБНЧШ§НЧаЮ![]() ЕФжБНЧЖЅЕу
ЕФжБНЧЖЅЕу![]() дкОиаЮ
дкОиаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЩЯЃЈЕу
ЩЯЃЈЕу![]() ВЛгыЕу
ВЛгыЕу![]() жиКЯЃЌПЩгыЕу
жиКЯЃЌПЩгыЕу![]() жиКЯЃЉЃЌТњзу
жиКЯЃЉЃЌТњзу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
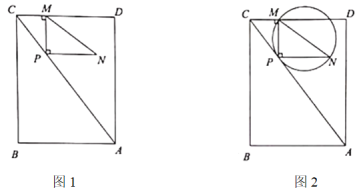
ЃЈ1ЃЉШє![]() ЃЌдђ
ЃЌдђ![]() ___________ЃЛ
___________ЃЛ
ЃЈ2ЃЉЕБЕу![]() дк
дк![]() ЕФЦНЗжЯпЩЯЪБЃЌЧѓ
ЕФЦНЗжЯпЩЯЪБЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ3ЃЉЕБЕу![]() ЕФЮЛжУЗЂЩњИФБфЪБЃК
ЕФЮЛжУЗЂЩњИФБфЪБЃК
ЂйШчЭМ2ЃЌ![]() ЕФЭтНгдВЪЧЗёгы
ЕФЭтНгдВЪЧЗёгы![]() вЛжББЃГжЯрЧаЃЎЫЕУїРэгЩЃЛ
вЛжББЃГжЯрЧаЃЎЫЕУїРэгЩЃЛ
ЂкжБНгаДГі![]() ЕФЭтНгдВгы
ЕФЭтНгдВгы![]() ЯрЧаЪБ
ЯрЧаЪБ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯBAC=90ЁуЃЌAB=ACЃЌADЁЭBCЃЌДЙзуЪЧDЃЌAEЦНЗжЁЯBADЃЌНЛBCгкЕуE.дкЁїABCЭтгавЛЕуFЃЌЪЙFAЁЭAEЃЌFCЁЭBC.
ЃЈ1ЃЉЧѓжЄЃКBE=CFЃЛ
ЃЈ2ЃЉдкABЩЯШЁвЛЕуMЃЌЪЙBM=2DEЃЌСЌНгMCЃЌНЛADгкЕуNЃЌСЌНгME.ЧѓжЄЃКЂйMEЁЭBCЃЛЂкDE=DN.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉНтВЛЕШЪН5x+2Ён3ЃЈxЉ1ЃЉЃЌВЂАбЫќЕФНтМЏдкЪ§жсЩЯБэЪОГіРДЃЎ
![]()
ЃЈ2ЃЉаДГівЛИіЪЕЪ§kЃЌЪЙЕУВЛЕШЪНxЃМkКЭЃЈ1ЃЉжаЕФВЛЕШЪНзщГЩЕФВЛЕШЪНзщЧЁга3ИіећЪ§НтЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдквЛеХОиаЮжНЦЌABCDжаЃЌAB=4ЃЌBC=8ЃЌЕуEЃЌFЗжБ№дкADЃЌBCЩЯЃЌНЋжНЦЌABCDбижБЯпEFелЕўЃЌЕуCТфдкADЩЯЕФвЛЕуHДІЃЌЕуDТфдкЕуGДІЃЌгавдЯТЫФИіНсТлЃКЂйHE=HFЃЛЂкECЦНЗжЁЯDCHЃЛЂлЯпЖЮBFЕФШЁжЕЗЖЮЇЮЊ3ЁмBFЁм4ЃЛЂмЕБЕуHгыЕуAжиКЯЪБЃЌEF=2![]() ЃЎвдЩЯНсТлжаЃЌФуШЯЮЊе§ШЗЕФгаЃЈЁЁЁЁЃЉИіЃЎ
ЃЎвдЩЯНсТлжаЃЌФуШЯЮЊе§ШЗЕФгаЃЈЁЁЁЁЃЉИіЃЎ
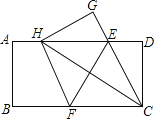
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊЩфЯп
ЮЊЩфЯп![]() ЩЯвЛЖЏЕуЃЈЕу
ЩЯвЛЖЏЕуЃЈЕу![]() ВЛгыЕу
ВЛгыЕу![]() жиКЯЃЉЃЎ
жиКЯЃЉЃЎ
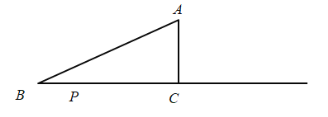
ЃЈ1ЃЉ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() зюЖЬЃЌЧѓГіДЫЪБ
зюЖЬЃЌЧѓГіДЫЪБ![]() ЕФзюаЁжЕЃЛ
ЕФзюаЁжЕЃЛ
ЃЈ2ЃЉ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЃЌЫЕУїРэгЩЃЛ
ЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБ![]() ЕФвЛИіЖЅЕугыЦфФкаФЁЂЭтаФдкЭЌвЛЬѕжБЯпЪБЃЌжБНгаДГі
ЕФвЛИіЖЅЕугыЦфФкаФЁЂЭтаФдкЭЌвЛЬѕжБЯпЪБЃЌжБНгаДГі![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇвпЧщЦкМфЮЊСЫЧаЪЕзЅКУЁАЭЃПЮВЛЭЃбЇЁБЛюЖЏЃЌНшжњФГШэМўЦНЬЈЫцЛњГщШЁСЫИУаЃВПЗжбЇЩњЕФдкЯпбЇЯАЪБМфЃЌВЂНЋНсЙћЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎ

ЧыФуИљОнвдЩЯаХЯЂЛиД№ЯТСаЮЪЬт
ЃЈ1ЃЉБОДЮЕїВщЕФШЫЪ§ЮЊЁЁЁЁЃЌ бЇЯАЪБМфЮЊ7аЁЪБЕФЫљЖдЕФдВаФНЧЮЊ ЃЛ
ЃЈ2ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉШєШЋаЃЙВгабЇЩњ1800ШЫЃЌЙРМЦгаЖрЩйбЇЩњдкЯпбЇЯАЪБМфВЛЕЭгк8ИіаЁЪБЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃФтЙКНјвЛХњЪжЖЏХчСмЯћЖОЩшБИЃЌвбжЊ1ИіAаЭХчЮэЦїКЭ2ИіBаЭХчЮэЦїЙВаш90дЊЃЛ2ИіAаЭХчЮэЦїКЭ3ИіBаЭХчЮэЦїЙВаш165дЊЃЎ
ЃЈ1ЃЉЮЪвЛИіAаЭХчЮэЦїКЭвЛИіBаЭХчЮэЦїЕФЕЅМлИїЪЧЖрЩйдЊ?
ЃЈ2ЃЉбЇаЃОіЖЈЙКНјСНжжаЭКХЕФХчЮэЦїЙВ60ИіЃЌВЂЧввЊЧѓBаЭХчЮэЦїЕФЪ§СПВЛФмЖргкAаЭХчЮэЦїЕФ4БЖЃЌЧыФуЩшМЦГізюЮЊЪЁЧЎЕФЙКТђЗНАИЃЌВЂЫЕУїРэгЩЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌADЪЧЁЯBACЕФЦНЗжЯпЃЌDEЦНааABНЛACгкЕуEЃЌDFЦНааACНЛABгкЕуFЃЌбгГЄFEНЛBCЕФбгГЄЯпгкЕуGЃЎ
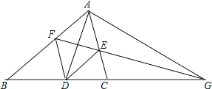
ЧѓжЄЃК
ЃЈ1ЃЉAGЃНDGЃЛ
ЃЈ2ЃЉЁЯGACЃНЁЯBЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com