练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在一个袋子里有1个红球9个白球，从中任意摸出1个球后不放回去，再从袋子里摸1个球，那么这次摸到红球的概率是多少？
    考点：列表法与树状图法
    专题：计算题
    分析：先画出树状图展示所有90种等可能的结果数，再找出第二次摸到红球的结果数，然后根据概率公式计算．
    解答：解：画树状图为：
    ，
    共有90种等可能的结果数，其中第二次摸到红球的结果数为9，
    所以再从袋子里摸1个球，那么这次摸到红球的概率=
    9
    90
    =
    1
    10
    ．
    点评：本题考查了列表法与树状图法：利用列表法或树状图法展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求解．注意从中任意摸出1个球后不放回．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    先化简：(
    1
    a-3
    +1)÷
    a2-4
    2a-6
    =
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在方格纸中建立适当的平面直角坐标系．
    （1）在所建坐标系中描出坐标是A（2，3），B（-2，3），C（3，-2），D（5，1），E（0，-4），F（-3，0）的各点；
    （2）计算图中线段EF的长和四边形ABCD的面积；
    （3）将线段AB向下平移6个单位，所得图形上任意一点的坐标可表示为
     
    （用字母x表示图形上点的横坐标）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

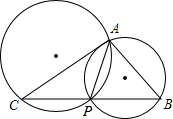    如图，已知，△ABC中，AB=4，AC=3，BC=6，P为BC边上一动点，则△ABP和△ACP的外接圆的半径之比为（　　）
    A、4﹕3
    B、3﹕2
    C、2﹕1
    D、不确定，与P点的位置有关

    查看答案和解析>>

    科目：初中数学 来源： 题型：

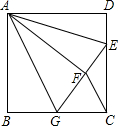    如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．下列结论：①BG=GC：②△ABG≌△AFG；③S△FGC=3；④AG∥CF．其中正确结论是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中，⊙P的圆心是（4，a）且（a＞2）半径为4，函数y=x的图象被⊙P截得的弦AB的长为4
    		3
    ，则a的值是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列事件是必然事件的是（　　）
    A、抛掷一枚硬币100次，有50次正面朝上
    B、面积相等的两个三角形全等
    C、a是实数，则|a|＞0
    D、方程x2-2x-100=0必有实数根

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    试写出一个开口向上，对称轴为直线x=-1，且与y轴的交点的坐标为（0，1）的抛物线的关系式
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列四组数中，其中都不是负数的是（　　）
    A、
    2
    7
    ，0，1.03
    B、-56，+3.1，
    45
    67
    C、-12，-7.5，0
    D、1，2，-0.23%

    查看答案和解析>>

    同步练习册答案