
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
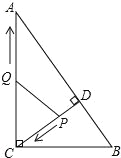
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:![]() =9:100?若存在,求出t的值;若不存在,则说明理由.
=9:100?若存在,求出t的值;若不存在,则说明理由.
(3)是否存在某一时刻t,使得△CPQ为等腰三角形?若存在,求出所有满足条件的t的值;若不存在,则说明理由.
【答案】(1)4.8(2)t=![]() 秒或t=3(3)存在,t为2.4秒或
秒或t=3(3)存在,t为2.4秒或![]() 秒或
秒或![]() 秒时
秒时
【解析】
试题分析:(1)利用勾股定理可求出AB长,再用等积法就可求出线段CD的长.
(2)过点P作PH⊥AC,垂足为H,通过三角形相似即可用t的代数式表示PH,从而可以求出S与t之间的函数关系式;利用![]() =9:100建立t的方程,解方程即可解决问题.
=9:100建立t的方程,解方程即可解决问题.
(3)可分三种情况进行讨论:由CQ=CP可建立关于t的方程,从而求出t;由PQ=PC或QC=QP不能直接得到关于t的方程,可借助于等腰三角形的三线合一及三角形相似,即可建立关于t的方程,从而求出t.
试题解析:(1)如图1,∵∠ACB=90°,AC=8,BC=6,
∴AB=10.
∵CD⊥AB,
∴S△ABC=![]() BC·AC=
BC·AC=![]() AB·CD.
AB·CD.
∴CD=![]() =
=![]() =4.8.
=4.8.
∴线段CD的长为4.8;
(2)①过点P作PH⊥AC,垂足为H,如图2所示.
由题可知DP=t,CQ=t.
则CP=4.8﹣t.
∵∠ACB=∠CDB=90°,
∴∠HCP=90°﹣∠DCB=∠B.
∵PH⊥AC,
∴∠CHP=90°.
∴∠CHP=∠ACB.
∴△CHP∽△BCA.
∴![]() .
.
∴![]() .
.
∴PH=![]() .
.
∴![]() =
=![]() CQ·PH=
CQ·PH=![]() t·(
t·(![]() )=
)=![]() ;
;
②存在某一时刻t,使得![]() =9:100.
=9:100.
∵![]() =
=![]() ×6×8=24,且
×6×8=24,且![]() =9:100,
=9:100,
∴(![]() ):24=9:100.
):24=9:100.
整理得:5t2﹣24t+27=0.
即(5t﹣9)(t﹣3)=0.
解得:t=![]() 或t=3.
或t=3.
∵0≤t≤4.8,
∴当t=![]() 秒或t=3秒时,
秒或t=3秒时,![]() =9:100;
=9:100;
(3)存在
①若CQ=CP,如图1,
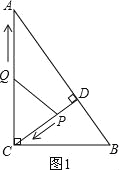
则t=4.8﹣t.
解得:t=2.4.
②若PQ=PC,如图2所示.
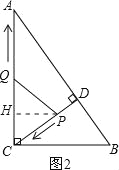
∵PQ=PC,PH⊥QC,
∴QH=CH=![]() QC=
QC=![]() .
.
∵△CHP∽△BCA.
∴![]() .
.
∴![]()
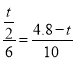 .
.
解得;t=![]() .
.
③若QC=QP,
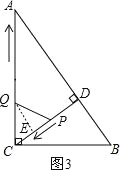
过点Q作QE⊥CP,垂足为E,如图3所示.
同理可得:t=![]() .
.
综上所述:当t为2.4秒或![]() 秒或
秒或![]() 秒时,△CPQ为等腰三角形.
秒时,△CPQ为等腰三角形.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】设计调查问卷时要注意( )
①问题应尽量简明;②不要提问被调查者不愿意回答的问题;③提问不能涉及提问者的个人观点;④提供的选择答案要尽可能全面;⑤问卷应简洁.
A.①②④⑤
B.①③④⑤
C.①②③④⑤
D.①⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下列各组线段为边,能组成三角形的是( )
A.1cm,2cm,4cmB.4cm,6cm,8cm
C.5cm,6cm,12cmD.2cm,3cm,5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列四个等式:①b﹣a=﹣(a﹣b);
②(a﹣b)4=(b﹣a)(b﹣a)3;③(a﹣b)3=﹣(b﹣a)3;④(a﹣b)3=(b﹣a)(a﹣b)2.其中恒成立的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品经过两次降价,每瓶零售价由168元降为108元,已知两次降价的百分率相同,设每次降价的百分率为x,根据题意列方程得( )
A.168(1+x)2=108
B.168(1﹣x)2=108
C.168(1﹣2x)=108
D.168(1﹣x2)=108
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com