
分析 (1)根据分式混合运算的法则把原式进行化简即可;
(2)根据a取2>a>-3的整数,分别求出所给的代数式的值;
(3)根据代数式为整数求出a的值即可.
解答 解:(1)原式=$\frac{{a}^{2}-4a+4}{a}$•$\frac{a(a+2)}{-(a+2)(a-2)}$•$\frac{1}{a+1}$
=$\frac{(a+2)(a-2)}{a}$•$\frac{a(a+2)}{-(a+2)(a-2)}$•$\frac{1}{a+1}$
=-$\frac{a+2}{a+1}$;
(2)∵a取2>a>-3的整数,
∴a=-2,-1,0,1,
当a=0,-1,-2时,原式无意义;
当a=1时,原式=-$\frac{1+2}{1+1}$=-$\frac{3}{2}$.
(3)∵-$\frac{a+2}{a+1}$为整数,
∴a=-2或a=0.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


科目:初中数学 来源: 题型:解答题
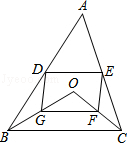 如图,点D,E分别是△ABC的边AB,AC的中点.点O是△ABC内的动点,点G,F分别是OB,OC的中点.
如图,点D,E分别是△ABC的边AB,AC的中点.点O是△ABC内的动点,点G,F分别是OB,OC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
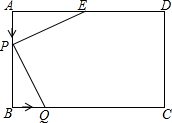 如图,已知矩形(即小学学过的长方形)ABCD中,AD=6cm,AB=4cm,点E为AD的中点.
如图,已知矩形(即小学学过的长方形)ABCD中,AD=6cm,AB=4cm,点E为AD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
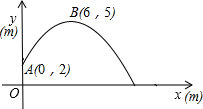 在体育测试时,初三(2)班的高个子张成同学推铅球,已知铅球所经过的路线是抛物线y=ax2+bx+c的一部分(如图所示),且知铅球出手处A点的坐标为(0,2)(单位:m,后同),铅球路线中最高处B点的坐标为(6,5)
在体育测试时,初三(2)班的高个子张成同学推铅球,已知铅球所经过的路线是抛物线y=ax2+bx+c的一部分(如图所示),且知铅球出手处A点的坐标为(0,2)(单位:m,后同),铅球路线中最高处B点的坐标为(6,5)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com