
【题目】如图,已知直线l:y=﹣x+4分别与x轴、y轴交于点A,B,双曲线![]() (k>0,x>0)与直线l不相交,E为双曲线上一动点,过点E作EG⊥x轴于点G,EF⊥y轴于点F,分别与直线l交于点C,D,且∠COD=45°,则k=_____.
(k>0,x>0)与直线l不相交,E为双曲线上一动点,过点E作EG⊥x轴于点G,EF⊥y轴于点F,分别与直线l交于点C,D,且∠COD=45°,则k=_____.

科目:初中数学 来源: 题型:
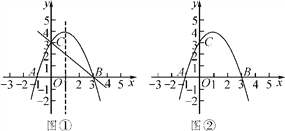
【题目】抛物线y=-x2+2x+3与x轴交于点A、B(点A在点B的左侧),与y轴交于点C.
(1)求直线BC的表达式;
(2)抛物线的对称轴上存在点P,使∠APB=∠ABC,利用图①求点P的坐标;
(3)点Q在y轴右侧的抛物线上,利用图②比较∠OCQ与∠OCA的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保,你我同行”.两年来,扬州市区的公共自行车给市民出行带来切实方便.电视台记者在某区街头随机选取了市民进行调查,调查的问题是“您大概多久使用一次公共自行车?”,将本次调查结果归为四种情况:A.每天都用;B.经常使用;C.偶尔使用;D.从未使用.将这次调查情况整理并绘制如下两幅统计图:

根据图中的信息,解答下列问题:
(1)本次活动共有 位市民参与调查;
(2)补全条形统计图;
(3)根据统计结果,若该区有46万市民,请估算每天都用公共自行车的市民约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】右图为手的示意图,在各个手指之间标记字母A,B,C,D。请你按图中箭头所指的方向(即A→B→C→D→C→B→A→B→C→……的方式)从A开始数连续的正整数1,2,3,4,5,6,7,8,9,……

(1)当数到14时,对应的字母是_________;
(2)当字母C第201次出现时。恰好数到的数是_________;
(3)当字母C第2n+1次出现时(n为正整数),恰好数到的数是__________(用含有n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
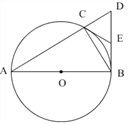
【题目】如图,已知ΔABC内接于⊙O,AB为⊙O的直径,BD⊥AB,交AC的延长线于点D.
(1)若E是BD的中点,连结CE,试判断CE与⊙O的位置关系.
(2)若AC=3CD,求∠A的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB和两点C、D,求作一点P,使PC=PD,且点P到∠AOB的两边的距离相等.
(要求:用尺规作图,保留作图痕迹,写出作法,不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=2![]() .
.
(1)利用尺规作线段AC的垂直平分线DE,垂足为E,交AB于点D;(保留作图痕迹,不写作法)
(2)若△ADE的周长为a,先化简T=(a+1)2﹣a(a﹣1),再求T的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:
第1行 1
第2行 -2 3
第3行 -4 5 -6
第4行 7 -8 9 -10
第5行 11 -12 13 -14 15
… …
按照上述规律排下去,那么第10行从左边数第5个数等于
A.50B.-50C.60D.-60
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com