
(本题10分)在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B作⊙O的切线BF交CD的延长线于点F,AC∥BF.
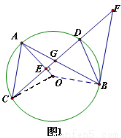


(1)如图1,求证:FG=FB;
(2)如图2,连接BD、AC,若BD=BG,求证:AC∥BF;
(3)在(2)的条件下,若tan∠F=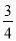 ,CD=1,求⊙O的半径
,CD=1,求⊙O的半径
(1)(2)证明见解析;(3)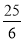
【解析】
试题分析:(1)连接OB,由BF是圆的切线可得直角,又有垂直,对顶角,利用等角的余角相等即可证;
(2)∠CAB和∠BDC都是弧BC所对的圆周角可证∠CAB=∠BDC,又可证∠DGB=∠GDB就可证∠CAB=∠GBF,即可证得平行;
(3)由平行可得∠ACE=∠F就得到tan∠F=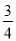 =tan∠ACE,由垂径定理可的CE=
=tan∠ACE,由垂径定理可的CE=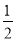 ,再由勾股定理求得AE,连接OE再用勾股定理求得半径.
,再由勾股定理求得AE,连接OE再用勾股定理求得半径.
试题解析:证明:(1)如图1
连接OB ∵BF是⊙O的切线
∴∠OBF=90°
∴∠OBA+∠GBF=90°
∵OA⊥CD
∴∠AEG=90° ∴∠AGE+∠EAG=90°
∵OA=OB
∴∠OAB=∠OBA
∴∠AGE=∠FBG
∵∠AGE=∠FGB
∴∠FGB=∠FBG
∴FG=FB
(2)∵BD=BG ∴∠DGB=∠GDB
∵∠CAB和∠BDC都是弧BC所对的圆周角
∴∠CAB=∠BDC
∴∠CAB=∠FGB
∵∠FGB=∠FBG
∴∠CAB=∠GBF
∴AC∥FB
【解析】
(3) 由(2)得∠FBG=∠CAG ∵∠FGB=∠FBG
∴∠CAG=∠FGB ∵∠FGB=∠CGA
∴∠CGA=∠CAG ∴CA=CG
∵AC∥BF∴∠ACE=∠F∴ tan∠ACE=tan∠F
∵tan∠F=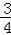 ∴tan∠ACE=
∴tan∠ACE=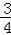 ∴
∴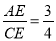
设AE=3k,则CE=4k. 在Rt△ACE中,
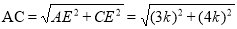 =5k
=5k
∴CG=5k
∴EG=CG-CE=5k-4k=k
∴k=1
∴CE=4,AE=3
连接OC,设⊙O的半径为R ,在Rt△CEO中,
CO2=CE2+OE 2 R2=42+(R-3) 2 解得R= 
即⊙O的半径为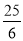 .
.
考点: 切线的性质定理,勾股定理,平行的判定.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源:2014-2015学年湖北省黄石市八年级9月月考数学试卷(解析版) 题型:填空题
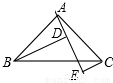
如图,在△ABC中,AB=AC,∠BAC=90°,AE是过A点的一条直线,CE⊥AE于E,BD⊥AE于D,DE=4cm,CE=2cm,则BD= 。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市顺义区八年级上学期期末考试数学试卷(解析版) 题型:选择题
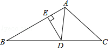
如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )
A.6 B.5 C.4 D.3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市顺义区八年级上学期期末考试数学试卷(解析版) 题型:选择题
在实数 ,
, ,
, 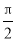 ,
, ,3.14中,无理数有( )
,3.14中,无理数有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省哈尔滨市道里区九年级上学期期末调研测试数学试卷(解析版) 题型:解答题
(本题7分) 先化简,再求值: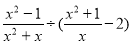 ,其中x=2cos30°+tan45.
,其中x=2cos30°+tan45.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省哈尔滨市道里区九年级上学期期末调研测试数学试卷(解析版) 题型:填空题
如图,在平行四边形ABCD中,E是边CD上一点,AE的延长线交BC的延长线于点F,请写出图中一对相似三角形:
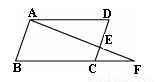
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省富阳市七年级1月单元问卷数学试卷(解析版) 题型:解答题
(本题8分)如图所示的3×3的方格中,画出4个面积小于9的不同的正方形,而且所画正方形的顶点都在方格的顶点上,并写出你所画的正方形的边长.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市阜宁县八年级上学期期中调研数学试卷(解析版) 题型:选择题
等边三角形中,两条中线所夹的锐角的度数为
A.30° B.40° C.50° D.60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com