
【题目】如图,AB是![]() 的一条弦,点C是
的一条弦,点C是![]() 上一动点,且
上一动点,且![]() ,点E、F分别是AC、BC的中点,直线EF与
,点E、F分别是AC、BC的中点,直线EF与![]() 交于G、H两点.若
交于G、H两点.若![]() 的半径为5,则
的半径为5,则![]() 的最大值为______.
的最大值为______.

【答案】7.5
【解析】
首先连接OA、OB,根据圆周角定理,求出∠AOB=2∠ACB=60°,进而判断出△AOB为等边三角形;然后根据⊙O的半径为5,可得AB=OA=OB=5,再根据三角形的中位线定理,求出EF的长度;最后判断出当弦GH是圆的直径时,它的值最大,进而求出GE+FH的最大值是多少即可.
如图1,连接OA、OB,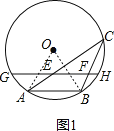 ,
,
∵∠ACB=30°,
∴∠AOB=2∠ACB=60°,
∵OA=OB,
∴△AOB为等边三角形,
∵⊙O的半径为5,
∴AB=OA=OB=5,
∵点E,F分别是AC、BC的中点,
∴EF=![]() AB=
AB=![]() ,
,
要求GE+FH的最大值,即求GE+FH+EF(弦GH)的最大值,
∵当弦GH是圆的直径时,它的最大值为:5×2=10,
∴GE+FH的最大值为:10-![]() =7.5.
=7.5.
故答案为:7.5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
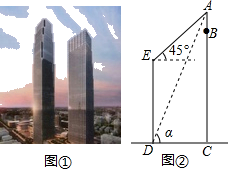
【题目】如图是长沙九龙仓国际金融中心,位于长沙市黄兴路与解放路交会处的东北角,投资160亿元人民币,总建筑面积达98万平方米,中心主楼BC高452m,是目前湖南省第一高楼,大楼顶部有一发射塔AB,已知和BC处于同一水平面上有一高楼DE,在楼DE底端D点测得A的仰角为α,tanα=![]() ,在顶端E点测得A的仰角为45°,AE=140
,在顶端E点测得A的仰角为45°,AE=140![]() m
m
(1)求两楼之间的距离CD;
(2)求发射塔AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了对学生进行革命传统教育,红旗中学开展了“清明节祭扫”活动.全校学生从学校同时出发,步行![]() 米到达烈士纪念馆.学校要求九
米到达烈士纪念馆.学校要求九![]() 班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的
班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的![]() 倍,结果比其他班提前
倍,结果比其他班提前![]() 分钟到达.分别求九(1)班、其他班步行的平均速度.
分钟到达.分别求九(1)班、其他班步行的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某水果公司以3元/kg的成本价新进10000kg柑橘,如果公司希望这批柑橘能获得利润6000元,已知柑橘损坏率统计表如下,请你填写最后一栏数据,完成此表:
(1)损坏率的概率约是多少,并说明理由 (保留小数点后一位)
(2)在出售柑橘(去掉损坏的柑橘)时,确定大约定价多少合适?
柑橘总质量 | 损坏柑橘质量 | 柑橘损坏的频率 |
300 | 30.9 | 0.103 |
350 | 35.7 | 0.102 |
400 | 39.2 | 0.098 |
450 | 44.5 | 0.099 |
500 | 50.5 | ? |
查看答案和解析>>
科目:初中数学 来源: 题型:
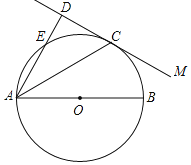
【题目】如图,AB是⊙O的直径,直线MC与⊙O相切于点C.过点A作MC的垂线,垂足为D,线段AD与⊙O相交于点E.
(1)求证:AC是∠DAB的平分线;
(2)若AB=10,AC=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界上大部分国家都使用摄氏温度(℃),但美、英等国的天气预报仍然使用华氏温度(℉),两种计量之间有如下的对应表:
摄氏温度(℃) | 0 | 10 | 20 | 30 | 40 | 50 |
华氏温度(℉) | 32 | 50 | 68 | 86 | 104 | 122 |
由上表可以推断出,华氏0度对应的摄氏温度是_____℃,若某一温度时华氏温度的值与对应的摄氏温度的值相等,则此温度为_____℃.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣2a2x(a≠0)的对称轴与x轴交于点P.
(1)求点P的坐标(用含a的代数式表示);
(2)记函数![]() (﹣1≤x≤3)的图象为图形M,若抛物线与图形M恰有一个公共点,结合函数的图象,求a的取值范围.
(﹣1≤x≤3)的图象为图形M,若抛物线与图形M恰有一个公共点,结合函数的图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
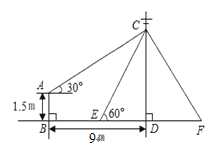
【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆9m的B处安置高为1.5m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留根号)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为![]() 的中点,P是直径MN上一动点,则PA+PB的最小值为( )
的中点,P是直径MN上一动点,则PA+PB的最小值为( )

A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com