
 如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.则∠ACH+∠ADH的值为( )
如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.则∠ACH+∠ADH的值为( )| BC |
| BH |
| BH |
| BD |
| 1 | ||
|
| AB2+AH2 |
| 2 |
| BC |
| BH |
| BH |
| BD |
| 1 | ||
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
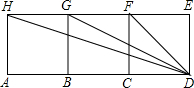 如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.请从图中找出二对相似三角形,要求其中一对必须不是直角三角形,并说明这一对三角形相似的理由.
如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.请从图中找出二对相似三角形,要求其中一对必须不是直角三角形,并说明这一对三角形相似的理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
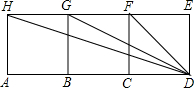 如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.请从图中找出二对相似三角形,要求其中一对必须不是直角三角形,并说明这一对三角形相似的理由.
如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.请从图中找出二对相似三角形,要求其中一对必须不是直角三角形,并说明这一对三角形相似的理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
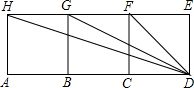
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com