
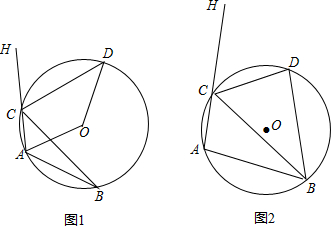
分析 (1)连接BD,由圆周角定理可知∠ABD=2∠ABD,要证明∠AOD=2∠BCD,即证明∠ABD=∠BCD,由圆内接四边形的性质和角平分线即可知∠HCD=∠BCD=∠ABD;
(2)由CB平分∠ACD可知∠ACB=∠DCB,所以$\widehat{AB}=\widehat{BD}$,从而可得AB=BD;
(3)由(2)可知△ABD是等边三角形,且⊙O的半径为$\frac{2\sqrt{15}}{3}$,所以AB的长度可求,连接OC并延长交⊙O于点E,连接AE,所以CE=$\frac{4\sqrt{15}}{3}$,利用tan∠ABC=tan∠E可求得AC的长度,设CN=x,由因为tan∠ABC=tan∠CDA,所以DN=2x,利用勾股定理列出方程即可求得x,进而求得CD的长度.
解答 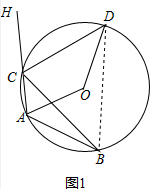 解:(1)如图1,连接BD,
解:(1)如图1,连接BD,
∵CD为△ABC的外角平分线,
∴∠HCD=∠BCD,
∵∠HCD=∠ABD,
∴∠ABD=∠BCD,
∵∠AOD=2∠ABD,
∴∠AOD=2∠BCD;
(2)∵CB平分∠ACD,
∴∠ACB=∠DCB,
∴$\widehat{AB}$=$\widehat{BD}$,
∴AB=BD;
(3) 连接OC并延长交⊙O于点E,连接AE,
连接OC并延长交⊙O于点E,连接AE,
过点O作OM⊥AB于点M,
过点C作CN⊥AD于点N,
由(2)可知:∠HCD=∠DCB=∠ACB=60°,
∴△ABD是等边三角形,
∴∠AOM=60°,
∵OA=$\frac{2\sqrt{15}}{3}$,
∴sin∠AOM=$\frac{AM}{OA}$,
∴AM=$\sqrt{5}$,
∴由垂径定理可知:AB=2AM=2$\sqrt{5}$,
∴AD=AB=2$\sqrt{5}$,
∵∠CEA=∠ABC,
∴tan∠CEA=tan∠ABC=$\frac{1}{2}$,
∴sin∠CEA=$\frac{\sqrt{5}}{5}$,
∴$\frac{AC}{CE}$=$\frac{\sqrt{5}}{5}$,
∴AC=$\frac{4}{3}$$\sqrt{3}$,
∵∠CDA=∠ABC,
∴tan∠CDA=$\frac{1}{2}$,
设CN=x,则DN=2x,
∴AN=2$\sqrt{5}$-2x,
∵由勾股定理可知:AC2=AN2+CN2,
∴$(\frac{4\sqrt{3}}{3})^{2}$=(2$\sqrt{5}$-2x)2+x2
∴x=$\frac{12\sqrt{5}+2\sqrt{15}}{15}$或x=$\frac{12\sqrt{5}-2\sqrt{15}}{15}$,
当x=$\frac{12\sqrt{5}+2\sqrt{15}}{15}$时,
∴DN=2x=$\frac{24\sqrt{5}+4\sqrt{15}}{15}$$>2\sqrt{5}$,
∴CN=$\frac{12\sqrt{5}-2\sqrt{15}}{15}$,
∵CD=$\sqrt{5}$x,
∴CD=$\frac{12-2\sqrt{3}}{3}$.
点评 本题考查圆的综合问题,涉及锐角三角函数,勾股定理,圆周角定理,垂径定理等知识,考查学生灵活运用知识的能力,解决本题的关键是连接OC并延长交⊙O于点E,连接AE构造直角△ACE.


科目:初中数学 来源: 题型:选择题
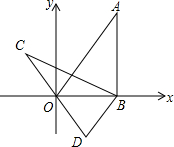 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )| A. | (-2,2$\sqrt{3}$) | B. | (-4,2$\sqrt{3}$) | C. | (-2$\sqrt{3}$,2) | D. | (-2$\sqrt{3}$,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
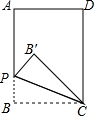 如图,在矩形ABCD中,AB=4,BC=3,点P是AB上(不含端点A,B)任意一点,把△PBC沿PC折叠,当点B′的对应点落在矩形ABCD的对角线上时,BP=$\frac{3}{2}$或$\frac{9}{4}$.
如图,在矩形ABCD中,AB=4,BC=3,点P是AB上(不含端点A,B)任意一点,把△PBC沿PC折叠,当点B′的对应点落在矩形ABCD的对角线上时,BP=$\frac{3}{2}$或$\frac{9}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
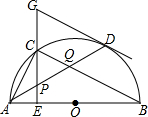 如图,AB是半圆O的直径,D是$\widehat{AB}$上一点,C是$\widehat{AD}$的中点,过点C作AB的垂线,交AB于E,与过点D的切线交于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:
如图,AB是半圆O的直径,D是$\widehat{AB}$上一点,C是$\widehat{AD}$的中点,过点C作AB的垂线,交AB于E,与过点D的切线交于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 假如小猫在如图所示的地板上自由地走来走去,并随意停留在某块方砖上,它最终停留在黑色方砖上的概率是( )
假如小猫在如图所示的地板上自由地走来走去,并随意停留在某块方砖上,它最终停留在黑色方砖上的概率是( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
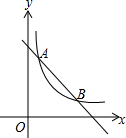 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(6,1),B(a,6)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(6,1),B(a,6)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com