

分析 (1)设抛物线顶点式解析式y=ax2+1,然后把点P的坐标代入进行计算即可得解;求出抛物线与x轴的交点A、B,然后利用待定系数法求一次函数解析式求出直线DB的解析式,令x=0求出y的值即可得到点D的坐标;
(2)根据四边形仅有一组对边平行,分①AP∥BE,求出直线AP的解析式,再根据平行直线的解析式的k值相等求出直线BE的解析式,与抛物线解析式联立求解即可得到点E的坐标;②AB∥PE,根据抛物线的对称性可得点E与点P关于y轴对称;③BP∥AE,根据平行直线的解析式的k值相等求出AE的解析式,与抛物线解析式联立求解即可得到点E的坐标;
(3)过点P作PM⊥x轴于点M,PN⊥y轴于点N,根据点A、B、P的坐标可以求出∠APM=60°,∠BPM=30°,∠APN=30°,然后求出PA是∠BPN的平分线,过点F作FH⊥PN于点H,连接DF、DH,根据角平分线上的点到角的两边的距离相等可得FH=m,根据三角形的三边关系可得当点D、F、H三点共线时,m+n的值最小,此时,点F为直线AP与y轴的交点,m+n=PN,然后求解即可.
解答 解:(1)∵抛物线顶点为C(0,2),
∴设抛物线的解析式是y=ax2+2,
又∵点P(4$\sqrt{3}$,-6)在抛物线上,
∴a(4$\sqrt{3}$)2+2=-6,
解得a=-$\frac{1}{6}$,
∴抛物线的解析式为y=-$\frac{1}{6}$x2+2;
令y=0,则-$\frac{1}{6}$x2+2=0,
解得x1=-2$\sqrt{3}$,x2=2$\sqrt{3}$,
∴点A(-2$\sqrt{3}$,0),点B(2$\sqrt{3}$,0),
设直线DP的解析式为y=kx+b,
则 $\left\{\begin{array}{l}{2\sqrt{3}k+b=0}\\{4\sqrt{3}k+b=-6}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{k=-\sqrt{3}}\\{b=6}\end{array}\right.$,
∴直线DP的解析式为y=-$\sqrt{3}$x+6,
令x=0,则y=6,
所以,点D的坐标为(0,6);
(2)①AP∥BE时,设直线AP的解析式为y=ex+f,
则 $\left\{\begin{array}{l}{-2\sqrt{3}e+f=0}\\{4\sqrt{3}e+f=-6}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{e=-\frac{\sqrt{3}}{3}}\\{f=-2}\end{array}\right.$,
所以,直线AP的解析式为y=-$\frac{\sqrt{3}}{3}$x-2,
设直线BE的解析式为y=-$\frac{\sqrt{3}}{3}$x+g,
则-$\frac{\sqrt{3}}{3}$×2$\sqrt{3}$+g=0,
解得g=2,
所以,直线BE的解析式为y=-$\frac{\sqrt{3}}{3}$x+2,
解$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}x+2}\\{y=-{\frac{1}{6}x}^{2}+2}\end{array}\right.$得 $\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=2\sqrt{3}}\\{{y}_{2}=0}\end{array}\right.$(为点B的坐标),
所以点E的坐标为(0,2);
②AB∥PE时,∵抛物线关于y轴对称,
∴点E为点P(4$\sqrt{3}$,-6)关于y轴的对称点,
∴点E(-4$\sqrt{3}$,-6);
③BP∥AE时,∵直线DP的解析式为y=-$\sqrt{3}$x+6,
∴设直线AE的解析式为y=-$\sqrt{3}$x+h,
则-$\sqrt{3}$×(-2$\sqrt{3}$)+h=0,
解得h=-6,
∴直线AE的解析式为y=-$\sqrt{3}$x-6,
解$\left\{\begin{array}{l}{y=-\sqrt{3}x-6}\\{y=-\frac{1}{6}{x}^{2}+2}\end{array}\right.$,得 $\left\{\begin{array}{l}{{x}_{1}=8\sqrt{3}}\\{{y}_{1}=-30}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-2\sqrt{3}}\\{{y}_{2}=0}\end{array}\right.$(为点A坐标),
所以,点E坐标为(8$\sqrt{3}$,-30),
综上所述,点E坐标为(0,2),(-4$\sqrt{3}$,-6),(8$\sqrt{3}$,-30); (3)如图,过点P作PM⊥x轴于点M,PN⊥y轴于点N,
(3)如图,过点P作PM⊥x轴于点M,PN⊥y轴于点N,
∵A(-2$\sqrt{3}$,0),B(2$\sqrt{3}$,0),P(4$\sqrt{3}$,-6),
∴tan∠APM=$\frac{AM}{PM}$=$\frac{6\sqrt{3}}{6}$=$\sqrt{3}$,
tan∠BPM=$\frac{BM}{PM}$=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$,
∴∠APM=60°,∠BPM=30°,
∴∠APB=∠APM-∠BPM=60°-30°=30°,
又∵PN∥AM,
∴∠APN=∠PAM=90°-60°=30°,
∴∠APB=∠APN,
点F在直线AP上,过点F作FH⊥PN于点H,根据角平分线的性质可得FH=m,
连接DF、DH,根据三角形的三边关系,DF+FH>DH,
即m+n>DH,
所以,当点D、F、H三点共线时,m+n的最小值,
此时,点F为直线AP与y轴的交点,点H、N重合,
最小值m+n=6-(-6)=6+6=12.
点评 本题是二次函数的综合题型,主要涉及待定系数法求函数解析式(二次函数与直线解析式),梯形的对边平行的性质,解直角三角形求锐角的度数,角平分线上的点到角的两边的距离相等的性质,以及三角形的三边关系,(1)利用顶点式解析式求解比较简单,(2)要注意分底边的不同进行讨论,(3)根据求出的角度的相等的角,利用角平分线的性质是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 甲代表队 | B. | 乙代表队 | C. | 丙代表队 | D. | 丁代表队 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
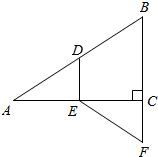 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=$\frac{1}{2}$BC.若AB=12,求EF的长.
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=$\frac{1}{2}$BC.若AB=12,求EF的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 31分 | B. | 33分 | C. | 36分 | D. | 38分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com