
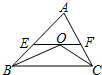
 如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )| A. | 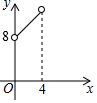 | B. | 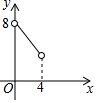 | C. | 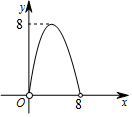 | D. | 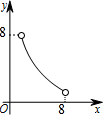 |
分析 由三角形的内心性质和平行线的性质证出BE=OE,CF=OF,得出△AEF的周长y与x的关系式为y=8-x,求出0<x<4,即可得出答案.
解答 解:∵点O是△ABC的内心,
∴∠ABO=∠CBO,∠ACO=∠BCO,
∵EF∥BC,
∴∠EOB=∠CBO,∠FOC=∠BCO,
∴∠ABO=∠EOB,∠ACO=∠FOC,
∴BE=OE,CF=OF,
∴△AEF的周长y=AE+EF+AF=AE+OE+OF+AF=AB+AC,
∵△ABC的周长为8,BC=x,
∴AB+AC=8-x,
∴y=8-x,
∵AB+AC>BC,
∴y>x,
∴8-x>x,
∴0<x<4,
即y与x的函数关系式为y=8-x(x<4),
故选:B.
点评 本题考查了动点问题的函数图象、三角形的内心、平行线的性质、等腰三角形的判定、三角形的周长等知识;求出y与x的关系式是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
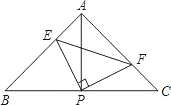 已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下结论:
已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下结论:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
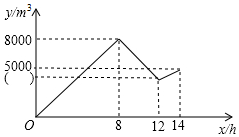 某企业一地下仓库发生渗水事故,凌晨0点开始渗漏,工作人员发现后于8点开始使用4台相同的抽水机排水,4小时后由于电路出现故障,为保证安全,有3台抽水机停止工作,2小时后电路故障仍然未完全排除,仅有两台抽水机恢复了工作,假设每小时的渗水量相同,仓库中的剩余水量不超过1000m3时才能对渗漏处进行封堵,仓库中存水量y(单位:m3)关于漏水时间x(单位:h)的函数图象如图所示.
某企业一地下仓库发生渗水事故,凌晨0点开始渗漏,工作人员发现后于8点开始使用4台相同的抽水机排水,4小时后由于电路出现故障,为保证安全,有3台抽水机停止工作,2小时后电路故障仍然未完全排除,仅有两台抽水机恢复了工作,假设每小时的渗水量相同,仓库中的剩余水量不超过1000m3时才能对渗漏处进行封堵,仓库中存水量y(单位:m3)关于漏水时间x(单位:h)的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
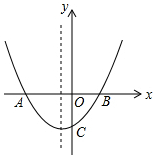 如图抛物线y=ax2+bx+c的图象交x轴于A(-2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
如图抛物线y=ax2+bx+c的图象交x轴于A(-2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
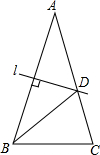 如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )
如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
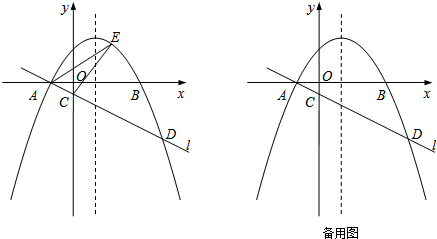
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
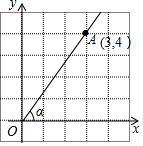 如图,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是( )
如图,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
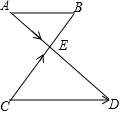 如图,已知AB∥CD,CD=2AB,AD、BC相交于点E,设$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{CE}$=$\overrightarrow{b}$,那么向量$\overrightarrow{CD}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为$\overrightarrow{b}$+2$\overrightarrow{a}$.
如图,已知AB∥CD,CD=2AB,AD、BC相交于点E,设$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{CE}$=$\overrightarrow{b}$,那么向量$\overrightarrow{CD}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为$\overrightarrow{b}$+2$\overrightarrow{a}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com