
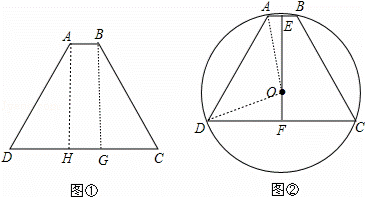
如图①,已知等腰梯形ABCD的周长为48,面积为S,AB∥CD,∠ADC=60°,设AB=3x.
(1)用x表示AD和CD;
(2)用x表示S,并求S的最大值;
(3)如图②,当S取最大值时,等腰梯形ABCD的四个顶点都在⊙O上,点E和点F分别是AB和CD的中点,求⊙O的半径R的值.
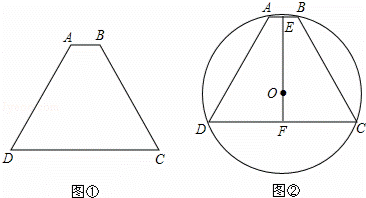
解:(1)作AH⊥CD于H,BG⊥CD于G,如图①,
则四边形AHGB为矩形,
∴HG=AB=3x,
∵四边形ABCD为等腰梯形,
∴AD=BC,DH=CG,
在Rt△ADH中,设DH=t,
∵∠ADC=60°,
∴∠DAH=30°,
∴AD=2t,AH=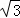 t,
t,
∴BC=2t,CG=t,
∵等腰梯形ABCD的周长为48,
∴3x+2t+t+3x+t+2t=48,解得t=8﹣x,
∴AD=2(8﹣x)=18﹣2x,
CD=8﹣x+3x+8﹣x=16+x;
(2)S=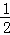 (AB+CD)•AH
(AB+CD)•AH
=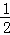 (3x+16+x)•
(3x+16+x)•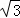 (8﹣x)
(8﹣x)
=﹣2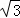 x2+8
x2+8 x+64
x+64 ,
,
∵S=﹣2 (x﹣2)2+72
(x﹣2)2+72 ,
,
∴当x=2时,S有最大值72 ;
;
(3)连结OA、OD,如图②,
当x=2时,AB=6,CD=16+2=18,等腰梯形的高为 ×(8﹣2)=6
×(8﹣2)=6 ,
,
则AE=3,DF=9,
∵点E和点F分别是AB和CD的中点,
∴直线EF为等腰梯形ABCD的对称轴,
∴EF垂直平分AB和CD,EF为等腰梯形ABCD的高,即EF=6 ,
,
∴等腰梯形ABCD的外接圆的圆心O在EF上,
设OE=a,则OF=6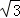 ﹣a,
﹣a,
在Rt△AOE中,
∵OE2+AE2=OA2,
∴a2+32=R2,
在Rt△ODF中,
∵OF2+DF2=OD2,
∴(6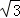 ﹣a)2+92=R2,
﹣a)2+92=R2,
∴a2+32=(6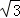 ﹣a)2+92,解得a=5
﹣a)2+92,解得a=5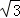 ,
,
∴R2=(5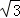 )2+32=84,
)2+32=84,
∴R=2
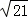 .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
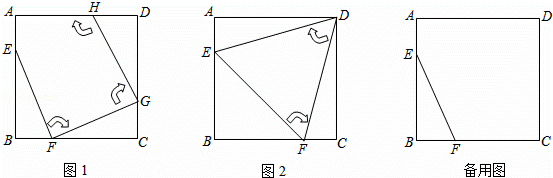
如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A,B重合),点F在BC边上(不与点B,C重合).
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;
依次操作下去…
(1)图2中的△EFD是经过两次操作后得到的,其形状为 ,求此时线段EF的长;
(2)若经过三次操作可得到四边形EFGH.
①请判断四边形EFGH的形状为 ,此时AE与BF的数量关系是 ;
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围;
(3)若经过多次操作可得到首尾顺次相接的多边形,其最大边数是多少?它可能是正多边形吗?如果是,请直接写出其边长;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
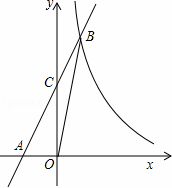
如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与x轴相交于点A(﹣2,0),与y轴交于点C,与反比例函数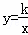 在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
(1)求一次函数的表达式;
(2)求反比例函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
贵阳市中小学幼儿园“爱心助残工程”第九届助残活动于2014年5月在贵阳市盲聋哑学校举行,活动当天,贵阳市盲聋哑学校获得捐赠的善款约为150000元.150000这个数用科学记数法表示为( )
|
| A. | 1.5×104 | B. | 1.5×105 | C. | 1.5×106 | D. | 15×104 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com