
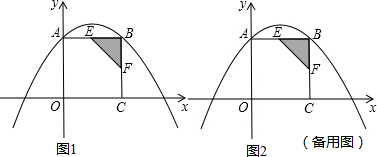
���� ��1�����ݵ�A��B�������3a-b=1���ô���ϵ��������������κ����Ľ���ʽ��
��2�����˶���ʼt��ʱ��EB=6-t��BF=t�����������ε������ʽ���ɵó�S����t�ĺ�����ϵʽ�������䷽�����ɵó���ֵ���⣻
�ڼ�����ڣ���Ϣٿɵó���E��F�����꣬�ֱ���BE��BF��EFΪ�Խ��߸���ƽ���ı��ε����������R�����꣬���ɵ�R�������������ö��κ���ͼ���ϵ���������ȷ����R�����꣬����ý⣮
��� �⣺��1����֪��A��0��6����B��6��6�����������ϣ���3a-b=-1��
��$\left\{\begin{array}{l}{6=c}\\{6=36a+6b+c}\\{3a-b=-1}\end{array}\right.$����ã�$\left\{\begin{array}{l}{a=-\frac{1}{9}}\\{b=\frac{2}{3}}\\{c=6}\end{array}\right.$��
����κ����Ľ���ʽΪy=-$\frac{1}{9}$x2+$\frac{2}{3}$x+6��
��2�����˶���ʼt��ʱ��EB=6-t��BF=t��
S=$\frac{1}{2}$BE•BF=$\frac{1}{2}$��6-t��t=-$\frac{1}{2}$t2+3t=-$\frac{1}{2}$��t-3��2+$\frac{9}{2}$��
��t=3ʱ��S�����ֵ$\frac{9}{2}$��
�ڼ�����ڣ���Sȡ�����ֵʱ���ɢ�֪t=3��
���E��3��6������F��6��3����
��E��B��R��FΪ������ı�����ƽ���ı��η������������ͼ����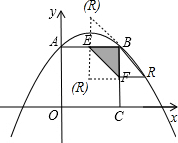
��i����BEΪ�Խ���ʱ��
�ߵ�B��6��6������E��3��6������F��6��3����
���R��6+3-6��6+6-3��������3��9����
��ii����BFΪ�Խ���ʱ��
�ߵ�B��6��6������E��3��6������F��6��3����
���R��6+6-3��6+3-6��������9��3����
��iii����EFΪ�Խ���ʱ��
�ߵ�B��6��6������E��3��6������F��6��3����
���R��6+3-6��6+3-6��������3��3����
�ߵ�R��������y=-$\frac{1}{9}$x2+$\frac{2}{3}$x+6�ϣ�
���R��������9��3����
���������ϴ��ڵ�R��9��3����ʹ���ı���EBRFΪƽ���ı��Σ�
���� ���⿼���˴���ϵ������������ʽ�������ε������ʽ�����κ����������Լ�ƽ���ı��ε����ʣ�����Ĺؼ��ǣ���1�����ô���ϵ���������������ʽ����2���ٸ��������ε������ʽ�ҳ�S����t�ĺ�����ϵʽ��������ƽ���ı��ε����������R�����꣮���������е��⣬�ѶȲ������������Ŀʱ������ƽ���ߵ����ʶԽ�����ƽ�ֽ���������������������ĸ�����������ǹؼ���


 һ����������ϵ�д�
һ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
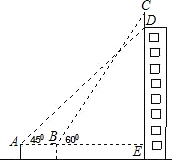 ��ͼij����¥������һ�����CD���ס������˷ֱ������8��A��B�������D���C������Ƿֱ�Ϊ45���60�㣬��A��B��E������һֱ�ߣ���AEC=90�㣩�ϣ���BE=15�ף���������Ƶ�CD����ȡ $\sqrt{3}$=1.73������������������
��ͼij����¥������һ�����CD���ס������˷ֱ������8��A��B�������D���C������Ƿֱ�Ϊ45���60�㣬��A��B��E������һֱ�ߣ���AEC=90�㣩�ϣ���BE=15�ף���������Ƶ�CD����ȡ $\sqrt{3}$=1.73�������������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����Ϊԭ����4�� | B�� | ����Ϊԭ����2�� | C�� | ���� | D�� | ��СΪԭ����$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | -2 | C�� | 1 | D�� | 1.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪����ƽ��ֱ������ϵ�У�A��-3��-4����B��0��-2����
��ͼ����֪����ƽ��ֱ������ϵ�У�A��-3��-4����B��0��-2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
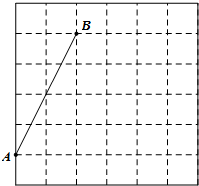 ��ͼ����ÿ��С�����εı߳���Ϊ1�ķ���ֽ�У����߶�AB����A��B����С�����εĶ����ϣ�
��ͼ����ÿ��С�����εı߳���Ϊ1�ķ���ֽ�У����߶�AB����A��B����С�����εĶ����ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com