
【题目】阅读下面材料,完成(1)﹣(3)题
数学课上,老师出示了这样一道题:如图,四边形ABCD,AD∥BC,AB=AD,E为对角线AC上一点,∠BEC=∠BAD=2∠DEC,探究AB与BC的数量关系.
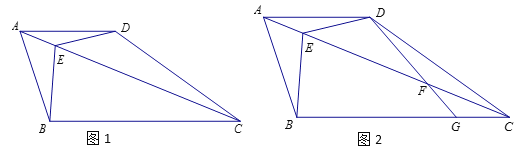
某学习小组的同学经过思考,交流了自己的想法:
小柏:“通过观察和度量,发现∠ACB=∠ABE”;
小源:“通过观察和度量,AE和BE存在一定的数量关系”;
小亮:“通过构造三角形全等,再经过进一步推理,就可以得到线段AB与BC的数量关系”.
……
老师:“保留原题条件,如图2, AC上存在点F,使DF=CF=![]() AE,连接DF并延长交BC于点G,求
AE,连接DF并延长交BC于点G,求![]() 的值”.
的值”.
(1)求证:∠ACB=∠ABE;
(2)探究线段AB与BC的数量关系,并证明;
(3)若DF=CF=![]() AE,求
AE,求![]() 的值(用含k的代数式表示).
的值(用含k的代数式表示).
【答案】(1)见解析;(2)CB=2AB;(3)![]()
【解析】
(1)利用平行线的性质以及角的等量代换求证即可;
(2)在BE边上取点H,使BH=AE,可证明△ABH≌△DAE,△ABE∽△ACB,利用相似三角形的性质从而得出结论;
(3)连接BD交AC于点Q,过点A作AK⊥BD于点K,得出![]() ,通过证明△ADK∽△DBC得出∠BDC=∠AKD=90°,再证DF=FQ,设AD=a,因此有DF=FC=QF=ka,再利用相似三角形的性质得出AC=3ka,
,通过证明△ADK∽△DBC得出∠BDC=∠AKD=90°,再证DF=FQ,设AD=a,因此有DF=FC=QF=ka,再利用相似三角形的性质得出AC=3ka,![]() ,
,![]() ,从而得出答案.
,从而得出答案.
解:(1)∵∠BAD=∠BEC
∠BAD=∠BAE+∠EAD
∠BEC=∠ABE+BAE
∴∠EAD=∠ABE
∵AD∥BC
∴∠EAD=∠ACB
∴∠ACB=∠ABE
(2)在BE边上取点H,使BH=AE
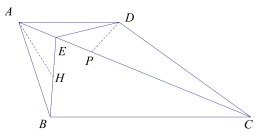
∵AB=AD
∴△ABH≌△DAE
∴∠AHB=∠AED
∵∠AHB+∠AHE=180°
∠AED+∠DEC=180°
∴∠AHE=∠DEC
∵∠BEC=2∠DEC
∠BEC=∠HAE+∠AHE
∴∠AHE=∠HAE
∴AE=EH
∴BE=2AE
∵∠ABE=∠ACB
∠BAE=∠CAB
∴△ABE∽△ACB
∴![]()
∴CB=2AB;
(3)连接BD交AC于点Q,过点A作AK⊥BD于点K
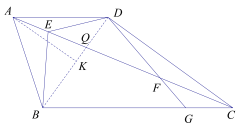
∵AD=AB
∴![]()
∠AKD=90°
∵![]()
∴![]()
∵AD∥BC
∴∠ADK=∠DBC
∴△ADK∽△DBC
∴∠BDC=∠AKD=90°
∵DF=FC
∴∠FDC=∠DFC
∵∠BDC=90°
∴∠FDC+∠QDF=90°
∠DQF+∠DCF=90°
∴DF=FQ
设AD=a
∴DF=FC=QF=ka
∵AD∥BC
∴∠DAQ=∠QCB
∠ADQ=∠QBC
∴△AQD∽△CQB
∴![]()
∴AQ=ka=QF=CF
∴AC=3ka
∵△ABE∽△ACB
∴![]()
∴![]()
同理△AFD∽△CFG
![]()
∴![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD、BC于E、F点,连结CE,若OC![]() cm,CD=4cm,则DE的长为( )
cm,CD=4cm,则DE的长为( )
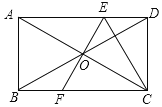
A.![]() cmB.5cmC.3cmD.2cm
cmB.5cmC.3cmD.2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,O为原点,点A(2,0),点P(1,m)(m>0)和点Q关于x轴对称.过点P作PB∥x轴,与直线AQ交于点B,如果AP⊥BO,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).

(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△OAB的三个顶点O(0,0)、A(4,1)、B(4,4)均在格点上.
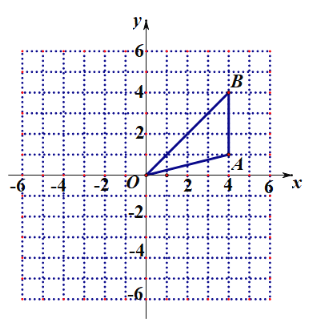
(1)画出△OAB绕原点![]() 顺时针旋转
顺时针旋转![]() 后得到的△
后得到的△![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
(2)在(1)的条件下,求线段![]() 在旋转过程中扫过的扇形的面积.
在旋转过程中扫过的扇形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,点E是AB的中点,点P是对角线AC上一动点,设PC的长度为x,PE与PB的长度和为y,图②是y关于x的函数图象,则图象上最低点H的坐标为_____.
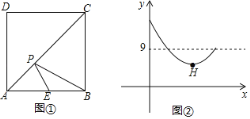
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
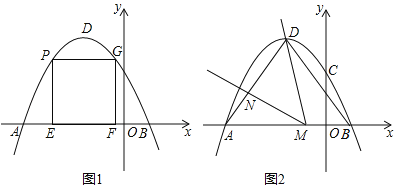
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)点![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一点,过点
之间的一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,当矩形
,当矩形![]() 的周长最大时,求点
的周长最大时,求点![]() 的横坐标;
的横坐标;
(3)如图2,连接![]() 、
、![]() ,点
,点![]() 在线段
在线段![]() 上(不与
上(不与![]() 、
、![]() 重合),作
重合),作![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() ,是否存在这样点
,是否存在这样点![]() ,使得
,使得![]() 为等腰三角形?若存在,求出
为等腰三角形?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
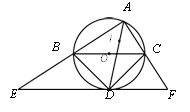
【题目】如图,A是以BC为直径的⊙O上一点,I是△ABC的内心,AI的延长线交⊙O于点D,过点D作BC的平行线交AB、AC的延长线于E、F.下列说法:①△DBC是等腰直角三角形;②EF与⊙O相切;③EF=2BC;④点B、I、C在以点D 为圆心的同一个圆上.其中一定正确的是_______(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】澜鑫商场为“双十一购物节”请甲乙两个广告公司布置展厅,已知乙单独完成此项任务的天数是甲单独完成此任务天数的2倍.若两公司合作4天,再由甲公司单独做3天就可以完成任务.
(1)甲公司与乙公司单独完成这项任务各需多少天?
(2)甲公司每天所需费用为5万元,乙公司每天所需费用为2万元,要使这项工作的总费用不超过40万元,则甲公司至多工作多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com