练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知：如图，平行四边形ABCD两条对角线AC、BD相交于点O，过O作一直线分别交AD、BC于点M、N，
    求证：OM=ON．

    【答案】分析：根据平行四边形的对角线互相平分可得OA=OC，再根据平行四边形的对边平行可得AD∥BC，利用两直线平行，内错角相等可得∠MAO=∠NCO，然后利用“角边角”证明△AMO和△CNO全等，根据全等三角形对应边相等即可得证．
    解答：证明：平行四边形ABCD中，OA=OC，AD∥BC，
    ∴∠MAO=∠NCO，
    在△AMO和△CNO中，，
    ∴△AMO≌△CNO（ASA），
    ∴OM=ON．
    点评：本题考查了平行四边形的对角线互相平分，对边平行的性质，全等三角形的判定与性质，比较简单．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （本题满分6分）已知：如图，E、F是平行四边行ABCD的对角线AC上的两点，AE=CF。

    求证：（1）△ADF≌△CBE；（2）EB∥DF。

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （本题满分6分）已知：如图，E、F是平行四边行ABCD的对角线AC上的两点，AE=CF。

    求证：（1）△ADF≌△CBE；（2）EB∥DF。

    查看答案和解析>>

    科目：初中数学 来源：2010-2011学年江苏省江阴市夏港中学九年级第二学期期中考试数学卷 题型：解答题

    （本题满分6分）已知：如图，E、F是平行四边行ABCD的对角线AC上的两点，AE=CF。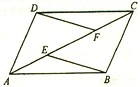

    求证：（1）△ADF≌△CBE；（2）EB∥DF。

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年山东省九年级上学期阶段检测数学卷（解析版） 题型：解答题

    已知：如图，E、F是平行四边行ABCD的对角线AC上的两点，AE=CF。

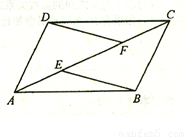
    求证：（1）△ADF≌△CBE；（2）EB∥DF。

    【解析】要证△ADF≌△CBE，因为AE=CF，则两边同时加上EF，得到AF=CE，又因为ABCD是平行四边形，得出AD=CB，∠DAF=∠BCE，从而根据SAS推出两三角形全等，由全等可得到∠DFA=∠BEC，所以得到DF∥EB

     

    查看答案和解析>>

    科目：初中数学 来源：2011届江苏省江阴市九年级第二学期期中考试数学卷 题型：解答题

    （本题满分6分）已知：如图，E、F是平行四边行ABCD的对角线AC上的两点，AE=CF。

    求证：（1）△ADF≌△CBE；（2）EB∥DF。

     

    查看答案和解析>>

    同步练习册答案