若抛物线y=x2-5x-6与x轴交于A、B两点,与y轴交于点C.
(1)求A、B、C三点坐标;
(2)画出大致图象;
(3)求△ABC的面积.
分析:(1)抛物线与x轴交于A、B两点,可令y=0,解得x即为两点坐标;与y轴交于点C,可令x=0,解得y即为C点坐标;
(2)根据(1)与坐标轴交点坐标,及抛物线图象性质即可画出大致图象;
(3)由坐标性质可确定三角形的高即为C点纵坐标的绝对值,再求AB长度即可求得三角形面积.
解答: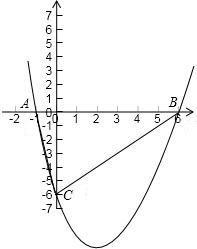
解:(1)由题意得:
令y=0,即x
2-5x-6=0,解得x
1=-1,x
2=6,
即A(-1,0),B(6,0);
令x=0,解得y=-6,即C(0,-6);
∴A(-1,0),B(6,0),C(0,-6);
(2)由(1)得.且抛物线开口向上,函数图象如图:
(3)由图象可知△ABC的面积S=
×AB×OC=
×7×6=21,
即三角形的面积为21;
点评:本题考查了二次函数图象坐标的特点及性质,要熟练掌握.

 解:(1)由题意得:
解:(1)由题意得:
