

分析 (1)结论PB=DN,欲证明PB=DN,只要证明△BAP≌△DAN即可.
(2)首先证明△BDN是RT△,在RT△BDN中理由勾股定理即可.
(3)分点M落在线段CD上或CD的延长线上两种情形讨论即可.
解答 解:(1)结论B=DN.
理由:如图1中,连接DN.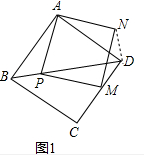
∵四边形ABCD、四边形APMN都是正方形,
∴AB=AD,AP=AN,∠BAD=∠PAN=90°,
∴∠BAP=∠DAN,
在△BAP和△DAN中,
$\left\{\begin{array}{l}{BA=DA}\\{∠BAP=∠DAN}\\{AP=AN}\end{array}\right.$,
∴△BAP≌△DAN,
∴PB=DN.
(2)如图2中,连接BN.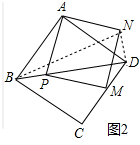
∵△BAP≌△DAN,
∴∠ABP=∠ADN=45°,BP=DN=1,
∵∠ADB=45°,
∴∠BDN=∠ADB+∠ADN=90°,
∵BD=2$\sqrt{2}$,
∴BN=$\sqrt{B{D}^{2}+D{N}^{2}}$=$\sqrt{(2\sqrt{2})^{2}+{1}^{2}}$=3.
(3)①如图3中,作AH⊥BD于H,MG⊥BD于G.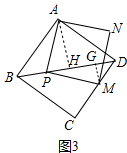
∵∠APH+∠MPG=90°,∠MPG+∠PMG=90°,
∴∠APH=∠PMG,∵∠AHP=∠PGM=90°,
∴△APH≌△PMG,
∴AH=PG,PH=MG,
∵AH=HD,
∴PG=DH,
∴PH=DG=GM,
∴∠GDM=45°,
∵∠DGC=45°,
∴点M在射线CD上.
②如图4中,作AH⊥BD于H,MG⊥BD于G.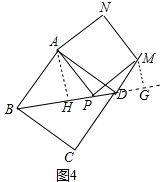
∵∠APH+∠MPG=90°,∠MPG+∠PMG=90°,
∴∠APH=∠PMG,∵∠AHP=∠PGM=90°,
∴△APH≌△PMG,
∴AH=PG,PH=MG,
∵AH=HD,
∴PG=DH,
∴PH=DG=GM,
∴∠GDM=45°,
∵∠DGC=45°,
∴点M在射线CD上.
综上所述点M在射线CD上.
点评 本题考查三角形综合题、正方形的性质、勾股定理等知识,解题的关键是正确寻找全等三角形,学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$ | C. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<4 | B. | 0<a<4 | C. | 0<a<10 | D. | a<10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com