【题目】如图所示，三角形ABC的面积为4cm2．AP垂直∠B的平分线BP于点P．则三角形PBC的面积是__．
【答案】2cm2
【解析】
过点P作PE⊥BP，垂足为P，交BC于点E，由角平分线的定义可知∠ABP=∠EBP，结合BP=BP以及∠APB=∠EPB=90°即可证出△ABP≌△EBP（ASA），进而可得出AP=EP，根据三角形的面积即可得出S△APC=S△EPC，再根据S△PBC=S△BPE+S△EPC=
S△ABC即可得出结论．
延长AP,交BC于点E,如图所示。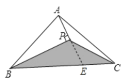
∵AP垂直∠B的平分线BP于点P，
∴∠ABP=∠EBP.
在△ABP和△EBP中,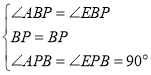 
，
∴△ABP≌△EBP(ASA)，
∴AP=EP.
∵△APC和△EPC等底同高，
S△PBC=S△BPE+S△EPC=S△ABC=2（cm2）.
故答案为2cm2.
科目：初中数学 来源： 题型：
【题目】已知点M是等边△ABD中边AB上任意一点(不与A. B重合),作∠DMN=60，交∠DBA外角平分线于点N.
(1)求证：DM=MN；
(2)若点M在AB的延长线上，其余条件不变，结论“DM=MN”是否依然成立?请你画出图形并证明你的结论.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，点E，F分别在边，AD，CD上，且
，BD和EF交于点O，延长BD至点H，使得
，并连接HE，HF．
求证：
；
试判断四边形BEHF是什么特殊的四边形，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店购进
、
两种商品，购买1个商品比购买1个商品多花10元，并且花费300元购买商品和花费100元购买商品的数量相等．
（1）求购买一个商品和一个商品各需要多少元；
（2）商店准备购买、两种商品共80个，若商品的数量不少于商品数量的4倍，并且购买、商品的总费用不低于1000元且不高于1050元，那么商店有哪几种购买方案？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】三台县某中学“五
四”青年节举行了“班班有歌声”歌咏比赛活动比赛聘请了10位教师和10位学生担任评委，其中甲班的得分情况如统计表和统计图．
老师评委评分统计表：
评委序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
分数 | 94 | 96 | 93 | 91 | x | 92 | 91 | 98 | 96 | 93 |
学生评委评分折线统计图师生评委评分频数分布直方图
补全频数分布直方图．
学生评委评分的中位数是______．
计分办法规定：老师评委、学生评委的评分各去掉一个最高分、一个最低分，并且按教师、学生各占
、
的方法计算各班最后得分，知甲班最后得分
分，试求统计表中的x．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料，解答下面的问题：
我们知道方程
有无数个解，但在实际问题中往往只需求出其正整数解．
例：由
，得：
( 
、
为正整数)．要使
为正整数，则
为正整数，可知： 
为3的倍数，从而
，代入
．所以的正整数解为
．
问题：
(1)请你直接写出方程
＝8的正整数解 ．
(2)若
为自然数，则满足条件的正整数
的值有( )
A．3个 B．4个 C．5个 D．6个
(3)关于
， 
的二元一次方程组
的解是正整数，求整数
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB=90°，∠CAB=30°．以AB长为一边作△ABD，且AD=BD，∠ADB=90°，取AB中点E，连DE、CE、CD．则∠EDC是多少度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在等边三角形ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP＝∠ACQ，BP＝CQ.
(1)求证：△ABP≌△ACQ；
(2)请判断△APQ是什么三角形，试说明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线
分别交x轴、y轴于A、B两点，抛物线
经过点A，和x轴的另一个交点为C．
求抛物线的解析式；
如图1，点D是抛物线上的动点，且在第三象限，求
面积的最大值；
如图2，经过点
的直线交抛物线于点P、Q，连接CP、CQ分别交y轴于点E、F，求
的值．
备注：抛物线顶点坐标公式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com