
 如图,点A、B的坐标分别为(0,2),(3,4),点P为x轴上的一点,若点B关于直线AP的对称点B′恰好落在x轴上,则点P的坐标为($\frac{4}{3},0$).
如图,点A、B的坐标分别为(0,2),(3,4),点P为x轴上的一点,若点B关于直线AP的对称点B′恰好落在x轴上,则点P的坐标为($\frac{4}{3},0$). 分析 先用待定系数法求出直线AB的解析式,由对称的性质得出AP⊥AB,求出直线AP的解析式,然后求出直线AP与x轴的交点即可.
解答 方法一:解:设直线AB的解析式为:y=kx+b,
把A(0,2),B(3,4)代入得:$\left\{\begin{array}{l}{b=2}\\{3k+b=4}\end{array}\right.$,
解得:k=$\frac{2}{3}$,b=2,
∴直线AB的解析式为:y=$\frac{2}{3}$x+2;
∵点B与B′关于直线AP对称,设B′坐标为(a,0)
∴线段BB′的中点坐标为($\frac{a+3}{2}$,2)
∵线段BB′的中点在直线AP上,且A点坐标为(0,2)
∴A点为线段BB′的中点,即A、B、B′三点共线
∴AP⊥AB,
∴设直线AP的解析式为:y=-$\frac{3}{2}$x+c,
把点A(0,2)代入得:c=2,
∴直线AP的解析式为:y=-$\frac{3}{2}$x+2,
当y=0时,-$\frac{3}{2}$x+2=0,
解得:x=$\frac{4}{3}$,
∴点P的坐标为:($\frac{4}{3},0$);
故答案为:($\frac{4}{3},0$).
方法二: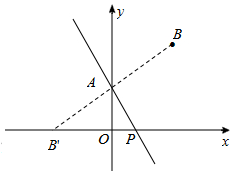 解:如图,连接AB、AB′
解:如图,连接AB、AB′
∵A(0,2),B(3,4)
∴AB=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$
∵点B与B′关于直线AP对称
∴AB′=AB=$\sqrt{13}$,
在Rt△AOB′中,B′O=$\sqrt{AB{′}^{2}-A{O}^{2}}$=3
∴B′点坐标为(-3,0)
设直线BB′方程为y=kx+b
将B(3,4),B′(-3,0)代入得:$\left\{\begin{array}{l}{3k+b=4}\\{-3k+b=0}\end{array}\right.$,
解得k=$\frac{2}{3}$,b=2
∴直线BB′的解析式为:y=$\frac{2}{3}$x+2,
∴直线AP的解析式为:y=-$\frac{3}{2}$x+2,
当yAP=0时,-$\frac{3}{2}$x+2=0,
解得:x=$\frac{4}{3}$,
∴点P的坐标为:($\frac{4}{3},0$);
故答案为:($\frac{4}{3},0$).
点评 本题是一次函数综合题目,考查了用待定系数法确定一次函数的解析式、轴对称的性质、垂线的关系等知识;本题有一定难度,综合性强,由直线AB的解析式进一步求出直线AP的解析式是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
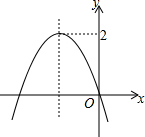 二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有两个不相等的实数根,则整数m的最小值为( )
二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有两个不相等的实数根,则整数m的最小值为( )| A. | -3 | B. | -2 | C. | -1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
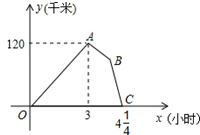 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下5个结论:
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下5个结论:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
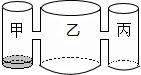 实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm).现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升$\frac{5}{6}$cm,则开始注入$\frac{3}{5}$,$\frac{33}{20}$,$\frac{171}{40}$分钟的水量后,甲与乙的水位高度之差是0.5cm.
实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm).现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升$\frac{5}{6}$cm,则开始注入$\frac{3}{5}$,$\frac{33}{20}$,$\frac{171}{40}$分钟的水量后,甲与乙的水位高度之差是0.5cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
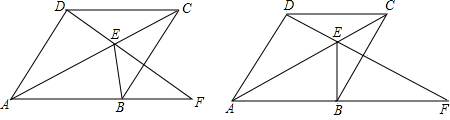
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
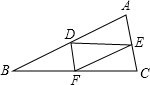 如图,在△ABC中,AB>AC,点D、E分别是边AB、AC的中点,点F在BC边上,连接DE、DF、EF,则添加下列哪一个条件后,仍无法判断△FCE与△EDF全等( )
如图,在△ABC中,AB>AC,点D、E分别是边AB、AC的中点,点F在BC边上,连接DE、DF、EF,则添加下列哪一个条件后,仍无法判断△FCE与△EDF全等( )| A. | ∠A=∠DFE | B. | BF=CF | C. | DF∥AC | D. | ∠C=∠EDF |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<1 | B. | 1<x<2 | C. | x>2 | D. | x<1或x>2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com