
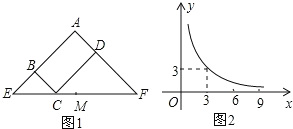
【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的序号是___.①当x=3时,EC<EM;②当y=9时,EC>EM③当x增大时,ECCF的值增大;④当y增大时,BEDF的值不变。
【答案】④
【解析】
由于等腰直角三角形AEF的斜边EF过C点,则△BEC和△DCF都是直角三角形;观察反比例函数图象得反比例解析式为y=![]() ;当x=3时,y=3,即BC=CD=3,根据等腰直角三角形的性质得CE=3
;当x=3时,y=3,即BC=CD=3,根据等腰直角三角形的性质得CE=3![]() ,CF=3
,CF=3![]() ,则C点与M点重合;当y=9时,根据反比例函数的解析式得x=1,即BC=1,CD=9,所以EF=10
,则C点与M点重合;当y=9时,根据反比例函数的解析式得x=1,即BC=1,CD=9,所以EF=10![]() ,而EM=5
,而EM=5![]() ;由于ECCF=
;由于ECCF=![]() x×
x×![]() y;利用等腰直角三角形的性质BEDF=BCCD=xy,然后再根据反比例函数的性质得BEDF=9,其值为定值.
y;利用等腰直角三角形的性质BEDF=BCCD=xy,然后再根据反比例函数的性质得BEDF=9,其值为定值.
因为等腰直角三角形AEF的斜边EF过C点,M为EF的中点,所以△BEC和△DCF都是直角三角形;
观察反比例函数图象得x=3,y=3,则反比例解析式为y=![]() ;
;
①、当x=3时,y=3,即BC=CD=3,所以CE=![]() BC=3
BC=3![]() ,CF=
,CF=![]() CD=3
CD=3![]() ,C点与M点重合,则EC=EM,所以①错误;
,C点与M点重合,则EC=EM,所以①错误;
②、当y=9时,x=1,即BC=1,CD=9,所以EC=![]() ,EF=10
,EF=10![]() ,EM=5
,EM=5![]() ,所以②错误;
,所以②错误;
③、因为ECCF=![]() x
x![]() y=2×xy=18,所以,ECCF为定值,所以③错误;
y=2×xy=18,所以,ECCF为定值,所以③错误;
④、因为BEDF=BCCD=xy=9,即BEDF的值不变,所以④正确.
故答案为:④.


科目:初中数学 来源: 题型:
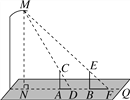
【题目】晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长(结果精确到0.01米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米,第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地,设第二组的步行速度为x千米/小时,根据题意可列方程是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店购进乒乓球拍和羽毛球拍进行销售,已知羽毛球拍比乒乓球拍每副进价高20元,用10000元购进羽毛球拍与用8000元购进乒乓球拍的数量相等.
(1)求每副乒乓球拍、羽毛球拍的进价各是多少元?
(2)该体育用品商店计划用不超过8840元购进乒乓球拍、羽毛球拍共100副进行销售,且乒乓球拍的进货量不超过60副,请求出该商店有几种进货方式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.

(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线y=![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
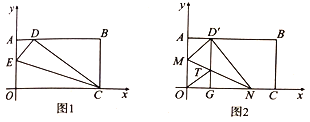
【题目】将一矩形纸片![]() 放在直角坐标系中,
放在直角坐标系中,![]() 为原点,点
为原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,![]() .
.
(1)如图1,在![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 折叠,使
折叠,使![]() 点落在
点落在![]() 边上的
边上的![]() 点处,求直线
点处,求直线![]() 的解析式;
的解析式;
(2)如图2,在![]() 边上选取适当的点
边上选取适当的点![]() ,将
,将![]() 沿
沿![]() 折叠,使
折叠,使![]() 点落在
点落在![]() 边上的点
边上的点![]() 处,过
处,过![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于
于![]() 点,连接
点,连接![]() ,判断四边形
,判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(3)、在(2)的条件下,若点![]() 坐标
坐标![]() ,点
,点![]() 在
在![]() 直线上,问坐标轴上是否存在点
直线上,问坐标轴上是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形,若存在,请直接写出点
为顶点的四边形是平行四边形,若存在,请直接写出点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=![]() x+
x+![]() 与y轴的交点为A,直线l1与直线l2:y=kx的交点M的坐标为M(3,a).
与y轴的交点为A,直线l1与直线l2:y=kx的交点M的坐标为M(3,a).
⑴a= ,k= ;
⑵直接写出关于x的不等式![]() x+
x+![]() ≥kx>0的解集 ;
≥kx>0的解集 ;
⑶若点B在x轴上,MB=MA,直接写出点B的坐标 .
⑷在x轴上是否存在一点N,使得NM-NA的值最大,若不存在,请说明理由;若存在,请直接写出点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b和反比例函数y2=![]() 的图象交于A、B两点.
的图象交于A、B两点.

(1)求一次函数y1=kx+b和反比例函数y2=![]() 的解析式;
的解析式;
(2)观察图象写出y1<y2时,x的取值范围为 ;
(3)求△OAB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com