
【题目】如图,已知AE是ΔABC的角平分线,AD是BC边上的高。若∠ABC=34°,∠ACB=64°,则∠DAE的大小是( )
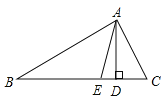
A. 5°B. 13°C. 15°D. 20°
科目:初中数学 来源: 题型:
【题目】某公司要将本公司100吨货物运往某地销售,经与运输公司协商,计划租用甲、乙两种型号的汽车共6辆,用这6辆汽车次将货物全部运走,其中每辆甲型汽车最多能装该种货物16吨,每辆乙型汽车最多能装该种货物18吨,已知租用1辆甲型汽车和2辆乙型汽车共需费用2600元;租用2辆甲型汽车和1辆乙型汽车共需费用2500元,且同一型号汽车每辆租车费用相同.
(1)求租用辆甲型汽车、一辆乙型汽车的费用分别是多少元?
(2)若这个公司计划此次租车费用不超过5200元,通过计算求出该公司有几种租车方案?请你设计出来,并求出最低的租车费用,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,方格图中每个小正方形的边长为1,点A、B、C都是格点.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)直接写出AA1的长度;
(3)如图2,A、C是直线MN同侧固定的点,D是直线MN上的一个动点,在直线MN上画出点D,使AD+DC最小.(保留作图痕迹)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李晖到“宇泉牌”服装专卖店做社会调查.了解到商店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员 | 小俐 | 小花 |
月销售件数(件) | 200 | 150 |
月总收入(元) | 1400 | 1250 |
假设月销售件数为![]() 件,月总收入为
件,月总收入为![]() 元,销售每件奖励
元,销售每件奖励![]() 元,营业员月基本工资为
元,营业员月基本工资为![]() 元.
元.
(1)求![]() 的值;
的值;
(2)若营业员小俐某月总收入不低于![]() 元,那么小俐当月至少要卖服装多少件?
元,那么小俐当月至少要卖服装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑经销商计划购进一批电脑机箱和液晶显示器,若购电脑机箱10台和液液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发生了求救信号,一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
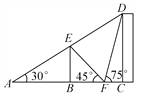
【题目】如图,楼房CD旁边有一池塘,池塘中有一电线杆BE高10米,在池塘边F处测得电线杆顶端E的仰角为45°,楼房顶点D的仰角为75°,又在池塘对面的A处,观测到A,E,D在同一直线上时,测得电线杆顶端E的仰角为30°.
(1)求池塘A,F两点之间的距离;
(2)求楼房CD的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个构造完全相同(除所标数字外)的转盘A、B.
(1)单独转动A盘,指向奇数的概率是 ;
(2)小红和小明做了一个游戏,游戏规定,转动两个转盘各一次,两次转动后指针指向的数字之和为奇数则小红获胜,数字之和为偶数则小明获胜,请用树状图或列表说明谁获胜的可能性大.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com