
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.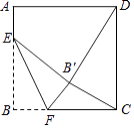
(1)当∠BEF=45°时,求证:CF=AE;
(2)当B′D=B′C时,求BF的长;
(3)求△CB′F周长的最小值.
【答案】
(1)
证明:如图1中,
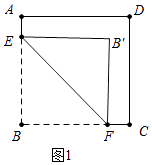
当∠BEF=45°时,易知四边形BEB′F是正方形,
∴BF=BE,
∵AB=BC,
∴CF=AE=3.
(2)
解:如图2中,作B′N⊥BC于N,NB′的延长线交AD于M,作EG⊥MN于G,则四边形MNCD、四边形AEGM都是矩形.
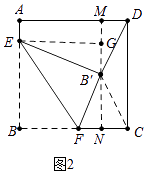
∵B′D=B′C,
∴∠B′DC=∠B′CD,
∵∠ADC=∠BCD=90°,
∴∠B′DM=∠B′CN,
∵∠B′MD=∠B′NC=90°,
∴△B′MD≌△B′CN,
∴B′M=B′N=8,
∵AE=MG=3,
∴GB′=5,
在Rt△EGB′中,EG= ![]() =
= ![]() =12,
=12,
∵∠EB′G+∠FB′N=90°,∠FB′N+∠B′FN=90°,
∴∠EB′G=∠B′FN,∵∠EGB′=∠FNB′=90°,
∴△EGB′∽△B′NF,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BF=B′F= ![]() .
.
(3)
解:如图3中,
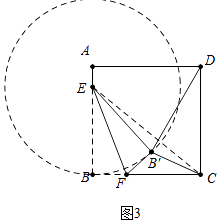
以E为圆心EB为半径画圆,在Rt△EBC中,∠EBC=90°,EB=13,BC=16,
∴EC= ![]() =5
=5 ![]() ,
,
∵△CFB′的周长=CF+FB′+CB′=BF+CF+CB′=BC+CB′=16+CB′,
∴欲求△CFB′的周长的最小值,只要求出CB′的最小值即可,
∵CB′+EB′≥EC,
∴E、B′、C共线时,CB′的值最小,CB′最小值为5 ![]() ﹣13.
﹣13.
∴△CFB′的周长的最小值为3+5 ![]() .
.
【解析】(1)如图1中,当∠BEF=45°时,易知四边形BEB′F是正方形,推出BF=BE,由AB=BC,即可证明CF=AE=3.(2)如图2中,作B′N⊥BC于N,NB′的延长线交AD于M,作EG⊥MN于G,则四边形MNCD、四边形AEGM都是矩形.由△B′MD≌△B′CN,推出B′M=B′N=8,由AE=MG=3,推出GB′=5,在Rt△EGB′中,EG= ![]() =
= ![]() =12,由△EGB′∽△B′NF,推出
=12,由△EGB′∽△B′NF,推出 ![]() =
= ![]() ,由此即可解决问题.(3)如图3中,以E为圆心EB为半径画圆,在Rt△EBC中,∠EBC=90°,EB=13,BC=16,推出EC=
,由此即可解决问题.(3)如图3中,以E为圆心EB为半径画圆,在Rt△EBC中,∠EBC=90°,EB=13,BC=16,推出EC= ![]() =5
=5 ![]() ,由△CFB′的周长=CF+FB′+CB′=BF+CF+CB′=BC+CB′=16+CB′,所以欲求△CFB′的周长的最小值,只要求出CB′的最小值即可,因为CB′+EB′≥EC,所以E、B′、C共线时,CB′的值最小.
,由△CFB′的周长=CF+FB′+CB′=BF+CF+CB′=BC+CB′=16+CB′,所以欲求△CFB′的周长的最小值,只要求出CB′的最小值即可,因为CB′+EB′≥EC,所以E、B′、C共线时,CB′的值最小.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为( )

A. 10 B. 6 C. 4 D. 不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义点P(a,b)的“变换点”为Q.且规定:当a≥b时,Q为(b,﹣a);当a<b时,Q为(a,﹣b).
(1)点(2,1)的变换点坐标为;
(2)若点A(a,﹣2)的变换点在函数y= ![]() 的图象上,求a的值;
的图象上,求a的值;
(3)已知直线l与坐标轴交于(6,0),(0,3)两点.将直线l上所有点的变换点组成一个新的图形记作M. 判断抛物线y=x2+c与图形M的交点个数,以及相应的c的取值范围,请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校合唱团有30名成员,下表是合唱团成员的年龄分布统计表:
年龄(单位:岁) | 13 | 14 | 15 | 16 |
频数(单位:名) | 5 | 15 | x | 10﹣x |
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A.平均数、中位数
B.平均数、方差
C.众数、中位数
D.众数、方差
查看答案和解析>>
科目:初中数学 来源: 题型:
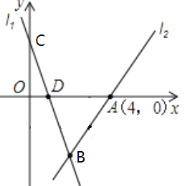
【题目】如图,直线l1:y=﹣3x+3交y轴于C,与x轴交于点D,直线l2经过点A(4,0),且直线l1、l2交于点B(2,m).
(1)求m的值和直线l2的函数表达式;
(2)直线l2在第一象限内的部分上有一点E,且△ADE的面积是△ADB面积的一半,求出点E的坐标,并在x轴上找一点P,使得CP+PE的值最小,求出这个最小值;
(3)若点Q为y轴上一点,且△BDQ为等腰三角形,请直接写出点Q的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一张三角形纸片ABC,其中∠C=90°,AC=6,BC=8.小静同学将纸片做两次折叠:第一次使点A落在C处,折痕记为m;然后将纸片展平做第二次折叠,使点A落在B处,折痕记为n.则m,n的大小关系是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com