
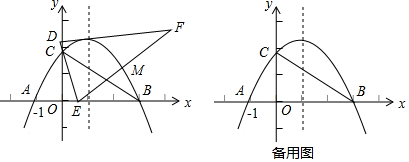
分析 (1)利用解直角三角形求出OC的长度,再求出OB的长度,从而可得点B、C的坐标,然后利用待定系数法求二次函数解析式解答;
(2)根据相似三角形对应边成比例列式求出OE的长度,再根据点A的坐标求出AO的长度,进而∠MEB=∠AEC=60°.即可得出结论;
(3)分在x轴上方和x轴上方两种情况,利用含30°的直角三角形的性质即可得出结论.
解答 解:(1)∵点A(-1,0),
∴OA=1,
由图可知,∠BAC是三角板的60°角,∠ABC是30°角,
所以,OC=OA•tan60°=1×$\sqrt{3}$=$\sqrt{3}$,
OB=OC•cot30°=$\sqrt{3}$×$\sqrt{3}$=3,
所以,点B(3,0),C(0,$\sqrt{3}$),
设抛物线解析式为y=ax2+bx+c,
则$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=\sqrt{3}}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=-\frac{\sqrt{3}}{3}}\\{b=\frac{2\sqrt{3}}{3}}\\{c=\sqrt{3}}\end{array}\right.$
所以,抛物线的解析式为y=-$\frac{\sqrt{3}}{3}$x2+$\frac{2\sqrt{3}}{3}$x+$\sqrt{3}$;
故答案为:3,0,0,$\sqrt{3}$;
(2)四边形AEMC是菱形.
∵△OCE∽△OBC,
∴$\frac{OE}{OC}=\frac{OC}{OB}$,
即$\frac{OE}{\sqrt{3}}=\frac{\sqrt{3}}{3}$,
解得OE=1,
∴E(1,0)在抛物线对称轴上,
∴△CAE为等边三角形,
∴∠AEC=∠A=60°.
又∵∠CEM=60°,
∴∠MEB=∠AEC=60°.
∴点C与点M关于抛物线的对称轴(x=1)对称.
C(0,$\sqrt{3}$),
∴M(2,$\sqrt{3}$).
∴MC=AE=2,MC∥AE
∴四边形AEMC是平行四边形.
∵AC=CM=2
∴四边形AEMC是菱形.
(3)由⊙P与直线AC和x轴同时相切,易知点P在两线夹角的平分线上,
①当在x轴上方时,如图,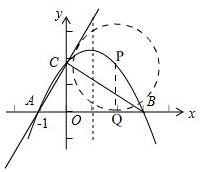 ∠PAO=30°,
∠PAO=30°,
设点P坐标为(m,-$\frac{\sqrt{3}}{3}$m2+$\frac{2\sqrt{3}}{3}$m+$\sqrt{3}$),
过P作PQ⊥x轴,交点为Q,则AQ=$\sqrt{3}$PQ,
得m+1=$\sqrt{3}$(-$\frac{\sqrt{3}}{3}$m2+$\frac{2\sqrt{3}}{3}$m+$\sqrt{3}$)
解得,m1=2,m2=-1(舍去),
所以点P坐标为(2,$\sqrt{3}$)
②当在x轴下方时,∠PAO=60°,
设点P坐标为(n,-$\frac{\sqrt{3}}{3}$n2+$\frac{2\sqrt{3}}{3}$n+$\sqrt{3}$),
过P'作P'Q'⊥x轴,交点为Q',
则$\sqrt{3}$AQ'=P'Q',得$\sqrt{3}$(n+1)=-(-$\frac{\sqrt{3}}{3}$n2+$\frac{2\sqrt{3}}{3}$n+$\sqrt{3}$)
解得,n1=6,n2=-1(舍去),
所以点P坐标为(6,-7$\sqrt{3}$)
综上所述,存在点P满足条件,点P坐标为(2,$\sqrt{3}$)或(6,-7$\sqrt{3}$).
点评 此题是二次函数综合题,主要考查了待定系数法,含30°的直角三角形的性质,菱形的判定和性质,圆的切线的性质,解(2)的关键是确定出点M的坐标,解(3)的关键是分两种情况,利用含30°的直角三角形的直线建立方程求解,是一道中等难度的中考常考题.


科目:初中数学 来源: 题型:选择题
| A. | 为了了解全市中学生课外阅读情况,选择全面调查 | |
| B. | 端午节期间,我市食品安全检查部门调查市场上粽子的质量情况,选择全面调查 | |
| C. | 旅客上飞机前的安检,选择抽样调查 | |
| D. | 为了了解《人民的名义》的收视率,选择抽样调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
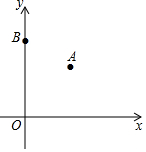 如图,在平面直角坐标系中,已知点A(3,3),B(0,5),若在坐标轴上找一点C,使得△ABC是等腰三角形,则这样的点C有( )
如图,在平面直角坐标系中,已知点A(3,3),B(0,5),若在坐标轴上找一点C,使得△ABC是等腰三角形,则这样的点C有( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 商品 | 售价(元/袋) |
| 芒果干 | 65 |
| 桂圆干 | 28 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com