
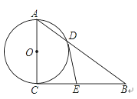
【题目】如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线,与边BC交于点E,若AD=![]() , AC=3.则DE长为( )
, AC=3.则DE长为( )
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
【答案】B
【解析】
连接OD,CD.由切线长定理得CD=DE,可证明△ADC∽△ACB,则可求得BD,再由勾股定理求得BC,可证明BE=DE,从而求得DE的长.
连接OD,CD.
∵AC为⊙O的直径,
∴∠ADC=90°,
∵AD=![]() ,AC=3.
,AC=3.
∴CD=![]() ,
,
∵OD=OC=OA,
∴∠OCD=∠ODC,
∵DE是切线,
∴∠CDE+∠ODC=90°.
∵∠OCD+∠DCB=90°,
∴∠BCD=∠CDE,
∴DE=CE.
∴△ADC∽△ACB,
∴∠B=∠ACD,
∴![]() ,
,
∴BC=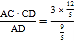 =4,
=4,
∵∠ACD+∠DCB=90°,
∴∠B+∠DCB=90°,∠B+∠CDE=90°,∠CDE+∠BDE=90°,
∴∠B=∠BDE,
∴BE=DE,
∴BE=CE=DE.
∴DE=![]() BC=
BC=![]() ×4=2.
×4=2.
故选:B.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
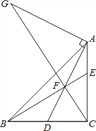
【题目】如图,Rt△ABC中,∠BCA=90°,AC=BC,点D是BC的中点,点F在线段AD上,DF=CD,BF交CA于E点,过点A作DA的垂线交CF的延长线于点G,下列结论:①CF2=EFBF;②AG=2DC;③AE=EF;④AFEC=EFEB.其中正确的结论有________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人轮流在黑板上写下不超过 ![]() 的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.
的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.
A. 10 B. 9 C. 8D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
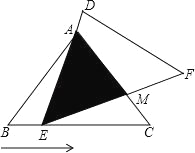
【题目】如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;
(3)当线段BE为何值时,线段AM最短,最短是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的月平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量江两岸码头B、D之间的距离,从山坡上高度为50米的A处测得码头B的俯角∠EAB为15°,码头D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求码头B、D的距离(结果保留整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于点C,抛物线的对称轴交
轴交于点C,抛物线的对称轴交![]() 轴于点D,已知A(-1,0),C(0,2) .
轴于点D,已知A(-1,0),C(0,2) .
(1)求抛物线的解析式;
(2)点E是线段BC上的一个动点(不与B、C重合),过点E作![]() 轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时点E的坐标.
轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时点E的坐标.
(3)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由.
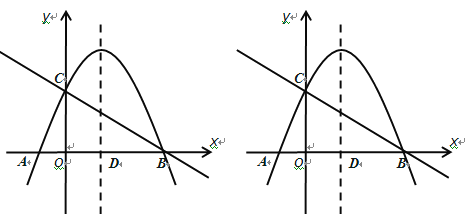
查看答案和解析>>
科目:初中数学 来源: 题型:
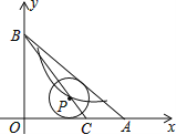
【题目】如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数![]() (k≠0)的图象经过圆心P,则k=________________。
(k≠0)的图象经过圆心P,则k=________________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com