
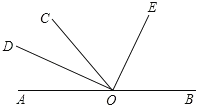
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)写出图中小于平角的角.
(2)求出∠BOD的度数.
(3)小明发现OE平分∠BOC,请你通过计算说明道理.
【答案】(1)答案见解析 (2)155° (3)答案见解析
【解析】
(1)根据角的定义即可解决;(2)根据∠BOD=∠DOC+∠BOC,首先利用角平分线的定义和邻补角的定义求得∠DOC和∠BOC即可;(3)根据∠COE=∠DOE﹣∠DOC和∠BOE=∠BOD﹣∠DOE分别求得∠COE与∠BOE的度数即可说明.
(1)图中小于平角的角∠AOD,∠AOC,∠AOE,∠DOC,∠DOE,∠DOB,∠COE,∠COB,∠EOB.
(2)因为∠AOC=50°,OD平分∠AOC,
所以∠DOC=25°,∠BOC=180°﹣∠AOC=180°﹣50°=130°,
所以∠BOD=∠DOC+∠BOC=155°.
(3)因为∠DOE=90°,∠DOC=25°,
所以∠COE=∠DOE﹣∠DOC=90°﹣25°=65°.
又因为∠BOE=∠BOD﹣∠DOE=155°﹣90°=65°,
所以∠COE=∠BOE,所以OE平分∠BOC.


科目:初中数学 来源: 题型:
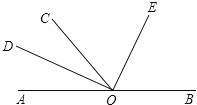
【题目】已知:如图1,把一张矩形纸片ABCD沿对角线BD折叠,将重合部分(△BFD)剪去,得到△ABF和△EDF.
(1)求证:FB=FD;
(2)求证:△ABF≌△EDF;
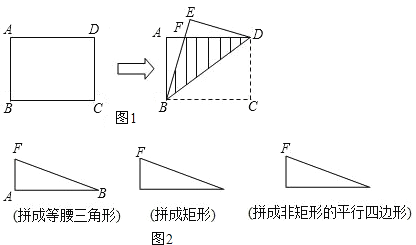
(3)将△ABF与△EDF不重合地拼在一起,可拼成特殊三角形和特殊四边形,请你按照下列要求将拼图补画完整(图2).
查看答案和解析>>
科目:初中数学 来源: 题型:
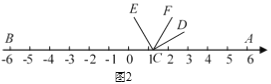
【题目】如图1,在数轴上A、B两点对应的数分别是6、﹣6,∠DCE=90°(C与O重合,D点在数轴的正半轴上).
(1)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.
①当t=1时,求α的度数;
②猜想∠BCE和α的数量关系,并证明;
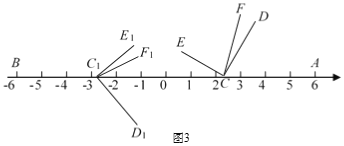
(2)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足![]() ,求出此时t的值.
,求出此时t的值.
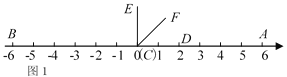
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列语句,画出图形.
(1)如图1,已知![]() 四点.
四点.
①画直线![]() ;
;
②连接线段![]() ,相交于点
,相交于点![]() ;
;
③画射线![]() ,相交于点
,相交于点![]() .
.
(2)如图2,有一个灯塔分别位于海岛![]() 的南偏西30°和海岛
的南偏西30°和海岛![]() 的南偏西60°的方向上,通过画图可推断灯塔的位置可能是
的南偏西60°的方向上,通过画图可推断灯塔的位置可能是![]() 四点中的____点.
四点中的____点.

查看答案和解析>>
科目:初中数学 来源: 题型:
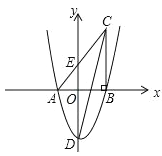
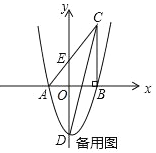
【题目】如图,在平面直角坐标系中,△ABC 的一边 AB 在 x 轴上,∠ABC=90°,点 C(4,8) 在第一象限内,AC 与 y 轴交于点 E,抛物线 y=![]() +bx+c 经过 A、B 两点,与 y 轴交于点 D(0,﹣6).
+bx+c 经过 A、B 两点,与 y 轴交于点 D(0,﹣6).
(1)请直接写出抛物线的表达式;
(2)求 ED 的长;
(3)若点 M 是 x 轴上一点(不与点 A 重合),抛物线上是否存在点 N,使∠CAN=∠MAN.若存在,请直接写出点 N 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B.乒乓球C.羽毛球 D.篮球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人,在扇形统计图中“D”对应的圆心角的度数为 ;
(2)请你将条形统计图补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,某同学早上8点坐车从余姚图书馆出发去宁波大学,汽车离开余姚图书馆的距离![]() (千米)与所用时间
(千米)与所用时间![]() (分)之间的函数关系如图所示.已知汽车在途中停车加油一次,则下列描述不正确的是( )
(分)之间的函数关系如图所示.已知汽车在途中停车加油一次,则下列描述不正确的是( )

A.汽车在途中加油用了10分钟
B.若![]() ,则加满油以后的速度为80千米/小时
,则加满油以后的速度为80千米/小时
C.若汽车加油后的速度是90千米/小时,则![]()
D.该同学![]() 到达宁波大学
到达宁波大学
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD、∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,则∠P的度数为( )
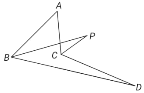
A. 10°B. 15°C. 20°D. 25°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=∠DOC=90°,OE平分∠AOD,反向延长射线OE至F.
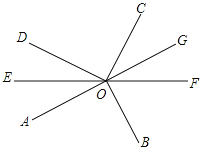
(1)∠AOD和∠BOC是否互补?说明理由;
(2)射线OF是∠BOC的平分线吗?说明理由;
(3)反向延长射线OA至点G,射线OG将∠COF分成了4:3的两个角,求∠AOD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com