Question

2．如图，矩形ABCD中，点E是边AB的中点，点F、G是分别边AD、BC上任意一点，且AE=BG，∠FEG=α．
（1）如图，若AE=AF，则EF与EG的数量关系为EF=EG，α=90°；
（2）在（1）的条件下，若点P为边BC上一点，连接EP，将线段EP以点E为旋转中心，逆时针旋转90°，得到线段EQ，连接FQ，在图2中补全图形，请猜想AF与BG的数量关系，并证明你的结论；
（3）在（2）的条件下，若∠EQF=30°，EF=$\sqrt{2}$a，则FQ=（$\sqrt{3}$-1）a（用含a的代数式表示）．

Answer 1

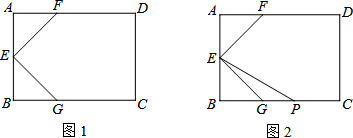
分析 （1）由矩形的性质得出∠A=∠B=90°，证出△AEF是等腰直角三角形，得出∠AEF=45°，由SAS证明△AEF≌△BEG，得出EF=EG，∠BEG=∠AEF=45°，得出∠FEG=90°即可；
（2）由旋转的性质得出∠QEP=90°，EQ=EP，由（1）得出∠FEG=90°，EF=EG，证出∠GEP=∠QEF，由SAS证明△EPG≌△EQF，得出对应边相等即可；
（3）作EM∥AD交QF的延长线于M，则∠M=90°，四边形AEMF是正方形，得出△MEF是等腰直角三角形，由三角函数求出MF、ME、QM，即可得出FQ．

解答 （1）解：EF与EG的数量关系为：EF=EG；α=90°；理由如下：
∵四边形ABCD是矩形，
∴∠A=∠B=90°，
∵点E是边AB的中点，
∴AE=BE，
∵AE=AF，
∴△AEF是等腰直角三角形，
∴∠AEF=45°，
∵AE=BG，
∴AE=BE=AF=BG，
△AEF在△AEF和△BEG中，
$\left\{\begin{array}{l}{AE=BE}&{\;}\\{∠A=∠B}&{\;}\\{AF=BG}&{\;}\end{array}\right.$，
∴△AEF≌△BEG（SAS），
∴EF=EG，∠BEG=∠AEF=45°，
∴∠FEG=180°-45°-45°=90°，
即α=90°，
故答案为：EF=EG；90°；
（2）解：补全图形，如图1所示：GP=FQ；理由如下：
由题意得：∠QEP=90°，EQ=EP，
由（1）得：∠FEG=90°，EF=EG，
∴∠GEP=∠QEF，
在△EPG和△EQF中，
$\left\{\begin{array}{l}{EG=EF}&{\;}\\{∠GEP=∠QEF}&{\;}\\{EP=EQ}&{\;}\end{array}\right.$，
∴△EPG≌△EQF（SAS），
∴GP=FQ；
（3）解：作EM∥AD交QF的延长线于M，如图2所示：
则∠M=90°，四边形AEMF是正方形，
∴△MEF是等腰直角三角形，
∴ME=MF=$\frac{\sqrt{2}}{2}$EF=a，
∵∠EQF=30°，
∴QM=$\sqrt{3}$ME=$\sqrt{3}$a，
∴FQ=QM-MF=$\sqrt{3}$a-a=（$\sqrt{3}$-1）a；
故答案为：（$\sqrt{3}$-1）a．

点评 本题是四边形综合题目，考查了矩形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、三角函数等知识；本题难度较大，综合性强，特别是（2）（3）中，需要画出图形，证明三角形全等和运用三角函数才能得出结果．