
 (
( ,
, )的图象经过点
)的图象经过点 (1,2),
(1,2), (
( ,
, )(
)( ),过点B作
),过点B作 轴的垂线,垂足为C.
轴的垂线,垂足为C.
 时,求点B的坐标;
时,求点B的坐标;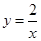 (2)(
(2)(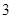 ,
,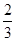 )(3)
)(3)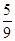 <a<3
<a<3 的图象经过点A(1,2) ∴
的图象经过点A(1,2) ∴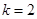 …………2分
…………2分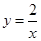 ………3分
………3分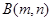 在
在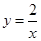 的图象上,∴
的图象上,∴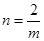 ,即
,即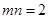 …………4分
…………4分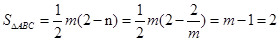 ,
,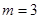 …………………… 5分
…………………… 5分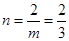
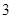 ,
,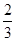 ) ……………………………………7分
) ……………………………………7分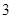 ,
,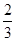 )分别代入y=ax-1得:a1=3,a2=
)分别代入y=ax-1得:a1=3,a2=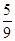
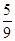 <a<3………………………………………………9分
<a<3………………………………………………9分

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
 的图象与反比例函数
的图象与反比例函数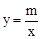 (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,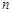 ).线段OA=5,E为x轴上一点,且sin∠AOE=
).线段OA=5,E为x轴上一点,且sin∠AOE= .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
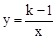 图象的两个分支分别位于第一、第三象限.
图象的两个分支分别位于第一、第三象限.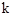 的取值范围;
的取值范围;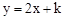 的图象与该反比例函数的图象有一个交点的纵坐标是4.
的图象与该反比例函数的图象有一个交点的纵坐标是4.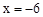 时反比例函数
时反比例函数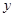 的值;
的值;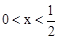 时,求此时一次函数
时,求此时一次函数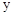 的取值范围.
的取值范围.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
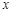 轴交于点C,与双曲线
轴交于点C,与双曲线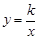 交于A(3,
交于A(3,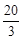 )、B(-5,
)、B(-5,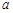 )两点.AD⊥
)两点.AD⊥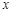 轴于点D,BE∥
轴于点D,BE∥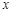 轴且与
轴且与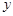 轴交于点E.
轴交于点E.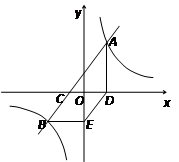
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
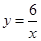 ,
,
| x | … | -6 | -5 | 3 | 4 | … |
| y | … | 1 | 1.2 | -2 | -1.5 | … |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
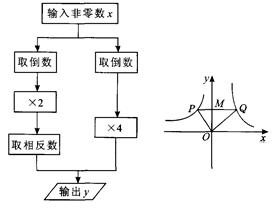
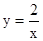 ,
,| A.①②④ | B.②④⑤ |
| C.③④⑤ | D.②③⑤ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
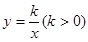 经过A、E两点,若AC:OB=1:3,梯形AOBC面积为24,则k=( )
经过A、E两点,若AC:OB=1:3,梯形AOBC面积为24,则k=( )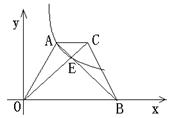
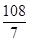 B、
B、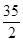 C、
C、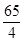 D、
D、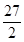
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 、
、 不是反比例的关系是( )
不是反比例的关系是( )A.书的单价为12元,售价 (元)与书的本数 (元)与书的本数 (本) (本) |
B. |
C.当 时,式子 时,式子 中的 中的 与 与 |
D.小亮上学用的时间 (分钟)与速度 (分钟)与速度 (米/分钟) (米/分钟) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com