
分析 (1)已知了抛物线的对称轴方程和抛物线与x轴两交点间的距离,可求出抛物线与x轴两交点的坐标;然后用待定系数法求出抛物线的解析式;
(2)把y=12代入求得的解析式,可求出抛物线上纵坐标为12的点的坐标.
解答 解:(1)设该抛物线的关系式为y=a(x-1)2+16,与x轴的两个交点的横坐标为x1<x2;
对称轴x=$\frac{{x}_{1}+{x}_{2}}{2}$=1,x2-x1=8;
解得:x1=-3,x2=5,
∴抛物线与x轴两交点为(-3,0),(5,0);
把点(5,0)代入y=a(x-1)2+16,得:16a+16=0,
∴a=-1;
∴该抛物线的关系式为y=-(x-1)2+16,
即y=-x2+2x+15;
(2)将y=12代入,得:-x2+2x+15=12;
解得x1=3,x2=-1;
∴这条抛物线上纵坐标为12的点的坐标为(3,12),(-1,12).
点评 本题考查了用待定系数法求函数解析式以及二次函数图象上点的坐标特征,根据题意求得与x轴的交点坐标是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
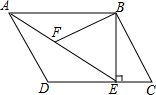 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.下列结论:
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.下列结论:| A. | ①②③④ | B. | ②③ | C. | ②④ | D. | ③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我国是世界上严重缺水的国家之一.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示.
我国是世界上严重缺水的国家之一.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
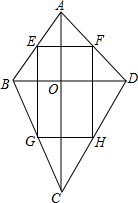 如图,四边形ABCD中,对角线AC⊥BD于点O,E、F、G、H分别是AB、AD、BC、CD的中点,
如图,四边形ABCD中,对角线AC⊥BD于点O,E、F、G、H分别是AB、AD、BC、CD的中点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com