
【题目】如图,已知![]() 中,
中,![]() ,AB=8cm,BC=6cm,P、Q是
,AB=8cm,BC=6cm,P、Q是![]() 边上的两个动点,其中点P从点A开始沿A
边上的两个动点,其中点P从点A开始沿A![]() B方向运动,且速度为每秒1cm,点Q从点B开始沿B
B方向运动,且速度为每秒1cm,点Q从点B开始沿B![]() C
C![]() A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1) 出发2秒后,求PQ的长;
(2) 当点Q在边BC上运动时,通过计算说明PQ能否把![]() 的周长平分?
的周长平分?
(3) 当点Q在边AC上运动时,求能使![]() 成为等腰三角形的运动时间.
成为等腰三角形的运动时间.
【答案】(1)2![]() cm;(2)点Q在边BC上运动时, PQ不能把△ABC的周长平分;(3)5.5秒或6秒或6.6秒.
cm;(2)点Q在边BC上运动时, PQ不能把△ABC的周长平分;(3)5.5秒或6秒或6.6秒.
【解析】
(1)根据点P、Q的运动速度求出AP,再求出BP和BQ,根据勾股定理即可求得PQ的长;
(2)由勾股定理求出AC,由题意得出方程,解方程求出t,即可得出结论;
(3)当点Q在边CA上运动时,能使△BCQ成为等腰三角形的运动时间有三种情况:
①当CQ=BQ时(图1),则∠C=∠CBQ,可证明∠A=∠ABQ,则BQ=AQ,则CQ=AQ,从而求得t;
②当CQ=BC时(图2),则BC+CQ=12,易求得t;
③当BC=BQ时(图3),过B点作BE⊥AC于点E,则求出BE,CE,即可得出t.
解:(1)BQ=2×2=4cm,
BP=AB-AP=8-2×1=6cm,
∵∠B=90°,
∴PQ=![]() =
=![]() =2
=2![]() (cm);
(cm);
(2)由勾股定理得:AC=![]() =
=![]() =10(cm),
=10(cm),
根据题意得:BQ=2tcm,CQ=(6-2t)cm,PA=tcm,BP=(8-t)cm,
若PQ能把△ABC的周长平分,则BQ+BP=CQ+PA+AC,
即2t+8-t=6-2t+t+10,
解得:t=4,
此时CQ=6-2t=-2,
∴t=4不合题意,
∴点Q在边BC上运动时, PQ不能把△ABC的周长平分;
(3)①当CQ=BQ时,如图1所示:

则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°,
∠A+∠C=90°,
∴∠A=∠ABQ
∴BQ=AQ,
∴CQ=AQ=5
∴BC+CQ=11,
∴t=11÷2=5.5秒;
②当CQ=BC时,如图2所示:

则BC+CQ=12
∴t=12÷2=6秒;
③当BC=BQ时,如图3所示:
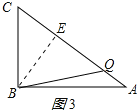
过B点作BE⊥AC于点E,
则BE=![]() =
=![]() =4.8(cm)
=4.8(cm)
∴CE=![]() =3.6cm,
=3.6cm,
∴CQ=2CE=7.2cm,
∴BC+CQ=13.2cm,
∴t=13.2÷2=6.6秒.
由上可知,当t为5.5秒或6秒或6.6秒时,
△BCQ为等腰三角形.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】近几年来,为了缓减环境污染,某区加大了对煤改电的投资力度,该区居民在2015年有7500户完成煤改电,2017年有10800户完成了煤改电.
(1)求该区2015年至2017年完成煤改电户数的年平均增长率;
(2)2018年该区计划要完成煤改电的户数比2017年要有所增长,但增长率不超过15%,请求出2018年最多有多少户能完成煤改电.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 和直线
和直线![]() .我们约定:当
.我们约定:当![]() 任取一值时,
任取一值时,![]() 对应的函数值
对应的函数值![]() 分别为
分别为![]() 、
、![]() ,若
,若![]() ,取
,取![]() 、
、![]() 中的较大值记为
中的较大值记为![]() ;若
;若![]() ,记
,记![]() .下列判断:
.下列判断:
①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() 值越大,
值越大,![]() 值越大;
值越大;
③使得![]() 的
的![]() 值不存在;④使
值不存在;④使![]() 的
的![]() 值有
值有![]() 个.
个.
其中正确的是________.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,D是BC中点,AD⊥BC,E是BC上除B,D,C外任意一点,根据“SAS”,可证明![]() ,所以AB=AC,∠B=∠C.在△ABE和△ACE中,
,所以AB=AC,∠B=∠C.在△ABE和△ACE中,![]() ,不能证明
,不能证明![]() ,因为这是“SSA”的情形,
,因为这是“SSA”的情形,![]() 是钝角三角形,
是钝角三角形,![]() 是锐角三角形,它们不可能全等.如果两个三角形都是直角三角形,“SSA”就变成“HL”,就可以用来证明两个三角形全等.同样,如果我们知道两个三角形都是钝角三角形或锐角三角形,并且它们满足“SSA”的情形,也是一定能全等的,但必须通过构造直角三角形来间接证明.
是锐角三角形,它们不可能全等.如果两个三角形都是直角三角形,“SSA”就变成“HL”,就可以用来证明两个三角形全等.同样,如果我们知道两个三角形都是钝角三角形或锐角三角形,并且它们满足“SSA”的情形,也是一定能全等的,但必须通过构造直角三角形来间接证明.
问题:已知,如图2,AD=AC,![]() ,
,
(1)根据现有条件直接证明![]() ,可以吗?为什么?
,可以吗?为什么?
(2)求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,![]() ),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为( )
),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2m+1)x+m(m+1)=0,
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两根分别为x1、x2,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句正确的有( )句
![]() 正方形都相似;
正方形都相似;![]() 有一个角对应相等的菱形相似;
有一个角对应相等的菱形相似;
![]() 有一个角相等的两个等腰三角形相似;
有一个角相等的两个等腰三角形相似;![]() 如果一个三角形有两个角分别为
如果一个三角形有两个角分别为![]() 和
和![]() ,另一个三角形有两个角分别为
,另一个三角形有两个角分别为![]() 和
和![]() ,那么这两个三角形可能不相似.
,那么这两个三角形可能不相似.
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两家运输公司规定每位旅客携带行李的费用与所带行李质量之间的关系图.

(1)由图可知,行李质量只要不超过______kg,甲公司就可免费携带,如果超过了规定的质量,则每超过1 kg要付运费_______元;
(2)解释图中点M所表示的实际意义;
(3)若设旅客携带的行李质量为x(kg),所付的行李费是y(元),请分别写出y甲与y乙(元)随x(kg)之间变化的关系式;
(4)若你准备携带45 kg的行李出行,在甲、乙两家公司中你会选择哪一家?应付行李费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请你用直尺和圆规作出这个输水管道的圆形截面的圆心(保留作图痕迹);
(2)若这个输水管道有水部分的水面宽AB=8 cm,水面最深地方的高度为2 cm,求这个圆形截面的半径.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com