
分析 (1)首先表示a与1的和为a+1,再表示是正数可得a+1>0;
(2)首先表示a的$\frac{1}{2}$和b的$\frac{1}{3}$的差为$\frac{1}{2}a$-$\frac{1}{3}b$,再表示“是负数”为$\frac{1}{2}a$-$\frac{1}{3}b$<0;
(3)首先表示a与b的两数和的平方为(a+b)2,再表示“不大于9”即可;
(4)首先表示a的$\frac{3}{2}$倍与b的和的平方为($\frac{3}{2}$a+b)2,再表示“是非负数”即可.
解答 解:(1)a+1>0;
(2)$\frac{1}{2}a$-$\frac{1}{3}b$<0;
(3)(a+b)2≤9;
(4)($\frac{3}{2}$a+b)2≥0.
点评 此题主要考查了由实际问题抽象出一元一次不等式,关键是要抓住题目中的关键词,如“大于(小于)、不超过(不低于)、是正数(负数)”“至少”、“最多”等等,正确选择不等号.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
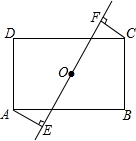 在矩形ABCD中,AB=8cm,AD=6cm,点O是矩形对角线交点,过O作任意一条直线,分别过点A、C作直线l的垂线,垂足为E、F.
在矩形ABCD中,AB=8cm,AD=6cm,点O是矩形对角线交点,过O作任意一条直线,分别过点A、C作直线l的垂线,垂足为E、F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
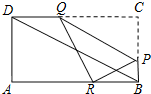 如图,在矩形ABCD中,AB=3,AD=$\sqrt{3}$,点P在边BC上的,过点P作PQ∥BD,交CD边于Q点,再把△PQC沿PQ对折,点C的对应点R恰好落在AB边上,则CP=$\frac{2\sqrt{3}}{3}$.
如图,在矩形ABCD中,AB=3,AD=$\sqrt{3}$,点P在边BC上的,过点P作PQ∥BD,交CD边于Q点,再把△PQC沿PQ对折,点C的对应点R恰好落在AB边上,则CP=$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一个正方体的表面展开如图所示,六个面上各有一字,连起来的意思是“预祝中考成功”,把它折成正方体后,与“考”相对的字是( )
一个正方体的表面展开如图所示,六个面上各有一字,连起来的意思是“预祝中考成功”,把它折成正方体后,与“考”相对的字是( )| A. | 预 | B. | 祝 | C. | 成 | D. | 功 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com