
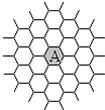
 用大小相同的正六边形瓷砖按如图所示的方式来铺设广场,中间的正六边形瓷砖记为A,定义为第一组,在它的周围铺上六块同样大小的正六边形瓷砖,定义为第二组,在第二组的外围用同样大小的正六边形瓷砖来铺满,定义为第三组,…,按这种方式铺下去,用现有的2005块瓷砖最多能完整地铺满________组,此时还剩余________块瓷砖.
用大小相同的正六边形瓷砖按如图所示的方式来铺设广场,中间的正六边形瓷砖记为A,定义为第一组,在它的周围铺上六块同样大小的正六边形瓷砖,定义为第二组,在第二组的外围用同样大小的正六边形瓷砖来铺满,定义为第三组,…,按这种方式铺下去,用现有的2005块瓷砖最多能完整地铺满________组,此时还剩余________块瓷砖.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
 20、用大小相同的正六边形瓷砖按如图所示的方式来铺设广场,中间的正六边形瓷砖记为A,定义为第一组,在它的周围铺上六块同样大小的正六边形瓷砖,定义为第二组,在第二组的外围用同样大小的正六边形瓷砖来铺满,定义为第三组,…,按这种方式铺下去,用现有的2005块瓷砖最多能完整地铺满
20、用大小相同的正六边形瓷砖按如图所示的方式来铺设广场,中间的正六边形瓷砖记为A,定义为第一组,在它的周围铺上六块同样大小的正六边形瓷砖,定义为第二组,在第二组的外围用同样大小的正六边形瓷砖来铺满,定义为第三组,…,按这种方式铺下去,用现有的2005块瓷砖最多能完整地铺满查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com