
”¾ĢāÄæ”æijŠ£æĘ¼¼Źµ¼łÉēĶÅÖĘ×÷Źµ¼łÉč±ø£¬Š”Ć÷µÄ²Ł×÷¹ż³ĢČēĻĀ
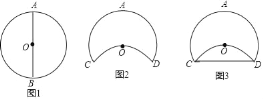
¢ŁŠ”Ć÷Č”³öĄĻŹ¦Ģį¹©µÄŌ²ŠĪĻøĢś»·£¬ĻČÕŅµ½Ō²ŠÄO£¬ŌŁČĪŅāÕŅ³öŌ²OµÄŅ»ĢõÖ±¾¶±ź¼ĒĪŖAB£ØČēĶ¼1£©£¬²āĮæ³öAB£½8·ÖĆ×£»
¢Ś½«Ō²»·½ųŠŠ·ÕŪŹ¹µćBĀäŌŚŌ²ŠÄOµÄĪ»ÖĆ£¬·ÕŪ²æ·ÖµÄŌ²»·ŗĶĪ“·ÕŪµÄŌ²»·²śÉś½»µć·Ö±š±ź¼ĒĪŖC”¢D£ØČēĶ¼2£©£®
¢ŪÓĆŅ»ĻøĻš½ŗ°ōĮ¬½ÓC”¢DĮ½µć£ØČēĶ¼3£©£»
¢Ü¼ĘĖć³öĻš½ŗ°ōCDµÄ³¤¶Č£®
Š”Ć÷¼ĘĖćĻš½ŗ°ōCDµÄ³¤¶ČĪŖ£Ø””””£©
A. 4![]() ·ÖĆ×B. 2
·ÖĆ×B. 2![]() ·ÖĆ×C. 2
·ÖĆ×C. 2![]() ·ÖĆ×D. 3
·ÖĆ×D. 3![]() ·ÖĆ×
·ÖĆ×

| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀ±ķ¼ĒĀ¼ĮĖŅ»ĆūĒņŌ±ŌŚ·£ĒņĻßÉĻĶ¶ĄŗµÄ½į¹ū£¬ÕāĆ“ĒņŌ±Ķ¶ĄŗŅ»“Ī£¬Ķ¶ÖŠµÄøÅĀŹŌ¼ŹĒ( )
Ķ¶Ąŗ“ĪŹż | 10 | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
Ķ¶ÖŠ“ĪŹż | 4 | 35 | 60 | 78 | 104 | 123 | 152 | 251 |
Ķ¶ÖŠĘµĀŹ | 0.40 | 0.70 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
A. 0.7B. 0.6C. 0.5D. 0.4
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŹŠŹµŹ©²śŅµ¾«×¼·öʶ£¬°ļ֜ʶĄ§»§³Š°ü»ÄɽÖÖÖ²Ä³Ę·ÖÖĆŪčÖ£®ŅŃÖŖøĆĆŪčֵijɱ¾¼ŪĪŖ6ŌŖ/Ē§æĖ£¬µ½ĮĖŹÕ»ń¼¾½ŚĶ¶ČėŹŠ³”ĻśŹŪŹ±£¬µ÷²éŹŠ³”ŠŠĒéŗ󣬷¢ĻÖøĆĆŪčÖ²»»įæ÷±¾£¬ĒŅĆæĢģµÄĻśŹŪĮæy£ØĒ§æĖ£©ÓėĻśŹŪµ„¼Ūx£ØŌŖ£©Ö®¼äµÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£®
£Ø1£©ĒóyÓėxµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³öxµÄȔֵ·¶Ī§£»
£Ø2£©µ±øĆĘ·ÖÖĆŪčֶؼŪĪŖ¶ąÉŁŹ±£¬ĆæĢģĻśŹŪ»ńµĆµÄĄūČó×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁ£æ
£Ø3£©Ä³“åÅ©»§½ńÄź¹²²ÉÕŖĆŪčÖ12000Ē§æĖ£¬ČōøĆĘ·ÖÖĆŪčֵı£ÖŹĘŚĪŖ50Ģģ£¬°“ÕÕ£Ø2£©µÄĻśŹŪ·½Ź½£¬ÄÜ·ńŌŚ±£ÖŹĘŚÄŚČ«²æĻśŹŪĶźÕāÅśĆŪčÖ£æČōÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£»Čō²»ÄÜ£¬Ó¦¶ØĻśŹŪ¼ŪĪŖ¶ąÉŁŌŖŹ±£¬¼ČÄÜĻśŹŪĶźÓÖÄÜ»ńµĆ×ī“óĄūČó£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
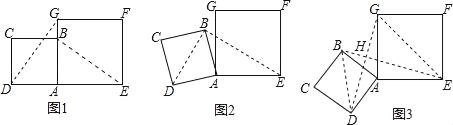
”¾ĢāÄæ”æŌŚŹżŃ§ŠĖȤŠ”×é»ī¶ÆÖŠ£¬Š”Ć÷½ųŠŠŹżŃ§Ģ½¾æ»ī¶Æ£¬½«±ß³¤ĪŖ2µÄÕż·½ŠĪABCDÓė±ß³¤ĪŖ2![]() µÄÕż·½ŠĪAEFG°“Ķ¼1Ī»ÖĆ·ÅÖĆ£¬ADÓėAEŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬ABÓėAGŌŚĶ¬Ņ»Ö±ĻßÉĻ£®
µÄÕż·½ŠĪAEFG°“Ķ¼1Ī»ÖĆ·ÅÖĆ£¬ADÓėAEŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬ABÓėAGŌŚĶ¬Ņ»Ö±ĻßÉĻ£®
£Ø1£©Š”Ć÷·¢ĻÖDG”ĶBE£¬ĒėÄć°ļĖūĖµĆ÷ĄķÓÉ£®
£Ø2£©ČēĶ¼2£¬Š”Ć÷½«Õż·½ŠĪABCDČʵćAÄꏱÕėŠż×Ŗ£¬µ±µćBĒ”ŗĆĀäŌŚĻ߶ĪDGÉĻŹ±£¬ĒėÄć°ļĖūĒó³ö“ĖŹ±BEµÄ³¤£®
£Ø3£©ČēĶ¼3£¬Š”Ć÷½«Õż·½ŠĪABCDČʵćA¼ĢŠųÄꏱÕėŠż×Ŗ£¬Ļ߶ĪDGÓėĻ߶ĪBE½«Ļą½»£¬½»µćĪŖH£¬Š“³ö”÷GHEÓė”÷BHDĆ껿֮ŗĶµÄ×ī“óÖµ£¬²¢¼ņŅŖĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
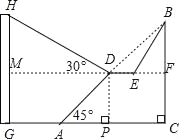
”¾ĢāÄæ”æĪŖµĖŠ”Ę½µ®³½110ÖÜÄźĻץń£¬¹ć°²ŹŠÕžø®¶Ō³ĒŹŠ½ØÉč½ųŠŠĮĖÕūøÄ£¬ČēĶ¼£¬ŅŃÖŖŠ±ĘĀAB³¤60![]() Ć×£¬ĘĀ½Ē(¼“”ĻBAC)ĪŖ45”ć£¬BC”ĶAC£¬ĻÖ¼Ę»®ŌŚŠ±ĘĀÖŠµćD“¦ĶŚČ„²æ·ÖŠ±ĘĀ£¬ŠŽ½ØŅ»øöĘ½ŠŠÓŚĖ®Ę½ĻßCAµÄŠŻĻŠĘ½ĢØDEŗĶŅ»ĢõŠĀµÄŠ±ĘĀBE(ĻĀĆęĮ½øöŠ”Ģā½į¹ū¶¼±£ĮōøłŗÅ)£®
Ć×£¬ĘĀ½Ē(¼“”ĻBAC)ĪŖ45”ć£¬BC”ĶAC£¬ĻÖ¼Ę»®ŌŚŠ±ĘĀÖŠµćD“¦ĶŚČ„²æ·ÖŠ±ĘĀ£¬ŠŽ½ØŅ»øöĘ½ŠŠÓŚĖ®Ę½ĻßCAµÄŠŻĻŠĘ½ĢØDEŗĶŅ»ĢõŠĀµÄŠ±ĘĀBE(ĻĀĆęĮ½øöŠ”Ģā½į¹ū¶¼±£ĮōøłŗÅ)£®
(1)ČōŠŽ½ØµÄŠ±ĘĀBEµÄĘĀ±ČĪŖ![]() £ŗ1£¬ĒóŠŻĻŠĘ½ĢØDEµÄ³¤ŹĒ¶ąÉŁĆ×£æ
£ŗ1£¬ĒóŠŻĻŠĘ½ĢØDEµÄ³¤ŹĒ¶ąÉŁĆ×£æ
(2)Ņ»×ł½ØÖžĪļGH¾ąĄėAµć33Ć×Ō¶(¼“AG£½33Ć×)£¬Š”ĮĮŌŚDµć²āµĆ½ØÖžĪļ¶„²æHµÄŃö½Ē(¼“”ĻHDM)ĪŖ30”ć£®µćB”¢C”¢A”¢G£¬HŌŚĶ¬Ņ»øöĘ½ĆęÄŚ£¬µćC”¢A”¢GŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬ĒŅHG”ĶCG£¬ĪŹ½ØÖžĪļGHøßĪŖ¶ąÉŁĆ×£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
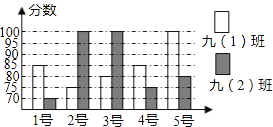
”¾ĢāÄæ”æĪŅĒųÄ³ÖŠŃ§æŖÕ¹”°Éē»įÖ÷ŅåŗĖŠÄ¼ŪÖµ¹Ū”±ŃŻ½²±ČČü»ī¶Æ£¬¾Å£Ø1£©”¢¾Å£Ø2£©°ąøł¾Ż³õČü³É¼Øø÷Ń”³ö5ĆūŃ”ŹÖ²Ī¼Óø“Čü£¬Į½øö°ąø÷Ń”³öµÄ5ĆūŃ”ŹÖµÄø“Čü³É¼Ø£ØĀś·ÖĪŖ100·Ö£©ČēĶ¼ĖłŹ¾£®øł¾ŻĶ¼ÖŠŹż¾Ż½ā¾öĻĀĮŠĪŹĢā£ŗ
£Ø1£©¾Å£Ø1£©°ąø“Čü³É¼ØµÄÖŠĪ»ŹżŹĒ”” ””·Ö£¬¾Å£Ø2£©°ąø“Čü³É¼ØµÄÖŚŹżŹĒ”” ””·Ö£»
£Ø2£©Š”Ć÷Ķ¬Ń§ŅŃ¾Ėć³öĮĖ¾Å£Ø1£©°ąø“ČüµÄĘ½¾ł³É¼Ø![]() =85·Ö£»·½²īS2=
=85·Ö£»·½²īS2=![]() [£Ø85©85£©2+£Ø75©85£©2+£Ø80©85£©2+£Ø85©85£©2+£Ø100©85£©2]=70£Ø·Ö2£©£¬ĒėÄćĒó³ö¾Å£Ø2£©°ąø“ČüµÄĘ½¾ł³É¼Øx2ŗĶ·½²īS22£»
[£Ø85©85£©2+£Ø75©85£©2+£Ø80©85£©2+£Ø85©85£©2+£Ø100©85£©2]=70£Ø·Ö2£©£¬ĒėÄćĒó³ö¾Å£Ø2£©°ąø“ČüµÄĘ½¾ł³É¼Øx2ŗĶ·½²īS22£»
£Ø3£©øł¾Ż£Ø2£©ÖŠ¼ĘĖć½į¹ū£¬·ÖĪöÄÄøö°ą¼¶µÄø“Čü³É¼Ø½ĻŗĆ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»Ö»Ļä×ÓĄļ¹²ÓŠ3øöĒņ£¬ĘäÖŠ2øö°×Ēņ£¬1øöŗģĒņ£¬ĖüĆĒ³żŃÕÉ«Ķā¾łĻąĶ¬”£
£Ø1£©“ÓĻä×ÓÖŠČĪŅāĆž³öŅ»øöĒņŹĒ°×ĒņµÄøÅĀŹŹĒ¶ąÉŁ£æ
£Ø2£©“ÓĻä×ÓÖŠČĪŅāĆž³öŅ»øöĒņ£¬²»½«Ėü·Å»ŲĻä×Ó£¬½ĮŌČŗóŌŁĆž³öŅ»øöĒņ£¬ĒóĮ½“ĪĆž³öĒņµÄ¶¼ŹĒ°×ĒņµÄøÅĀŹ£¬²¢»³öŹ÷דĶ¼”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
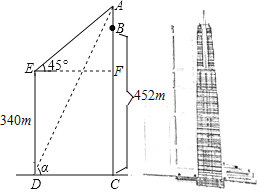
”¾ĢāÄæ”æČēĶ¼£¬³¤É³¾ÅĮś²Ö¹ś¼Ź½šČŚÖŠŠÄÖ÷Ā„BCøß“ļ452m£¬ŹĒÄæĒ°ŗžÄĻŹ”µŚŅ»øßĀ„£¬ŗĶĖü“¦ÓŚĶ¬Ņ»Ė®Ę½ĆęÉĻµÄµŚ¶žøßĀ„DEøß340m£¬ĪŖĮĖ²āĮæøßĀ„BCÉĻ·¢ÉäĖžABµÄøß¶Č£¬ŌŚĀ„DEµ×¶ĖDµć²āµĆAµÄŃö½ĒĪŖ¦Į£¬ŌŚ¶„¶ĖEµć²āµĆAµÄŃö½Ē”ĻAEF=45”ć£¬
£Ø1£©ČōÉčABĪŖxĆ×£¬ĒėÓĆŗ¬xµÄ“śŹżŹ½±ķŹ¾AFµÄ³¤£®
£Ø2£©Ēó³ö·¢ÉäĖžABµÄøß¶Č£®£Øcos¦Į”Ö![]() £¬sin¦Į”Ö
£¬sin¦Į”Ö![]() £¬tan¦Į”Ö
£¬tan¦Į”Ö![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻß¾¹żµć![]() £¬
£¬![]() £¬
£¬![]() £®
£®
![]() ĒóÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
ĒóÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
![]() ĒóÅ×ĪļĻߵĶ„µć×ų±ź£»
ĒóÅ×ĪļĻߵĶ„µć×ų±ź£»
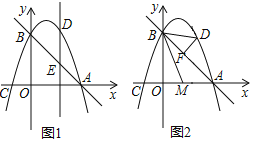
![]() ČēĶ¼1£¬µćDŹĒÅ×ĪļĻßÉĻŅ»¶Æµć£¬¹żD×÷yÖįµÄĘ½ŠŠĻßDE½»Ö±ĻßABÓŚµćE£¬µ±Ļ߶Ī
ČēĶ¼1£¬µćDŹĒÅ×ĪļĻßÉĻŅ»¶Æµć£¬¹żD×÷yÖįµÄĘ½ŠŠĻßDE½»Ö±ĻßABÓŚµćE£¬µ±Ļ߶Ī![]() Ź±£¬ĒėÖ±½ÓŠ“³öDµćµÄŗį×ų±ź£»
Ź±£¬ĒėÖ±½ÓŠ“³öDµćµÄŗį×ų±ź£»
![]() ČēĶ¼2£¬µ±DĪŖÖ±ĻßABÉĻ·½Å×ĪļĻßÉĻŅ»¶ÆµćŹ±£¬
ČēĶ¼2£¬µ±DĪŖÖ±ĻßABÉĻ·½Å×ĪļĻßÉĻŅ»¶ÆµćŹ±£¬![]() ÓŚF£¬ÉčACµÄÖŠµćĪŖM£¬Į¬½ÓBD£¬BM£¬ŹĒ·ń“ęŌŚµćD£¬Ź¹µĆ
ÓŚF£¬ÉčACµÄÖŠµćĪŖM£¬Į¬½ÓBD£¬BM£¬ŹĒ·ń“ęŌŚµćD£¬Ź¹µĆ![]() ÖŠÓŠŅ»øö½ĒÓė
ÖŠÓŠŅ»øö½ĒÓė![]() ĻąµČ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćDµÄŗį×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
ĻąµČ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćDµÄŗį×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com