
【题目】如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.、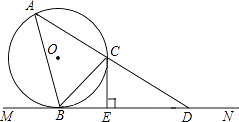
(1)求证:CE是⊙O的切线;
(2)若∠D=30°,BD=4,求⊙O的半径r.
【答案】
(1)证明:连接OC、OB,如图,
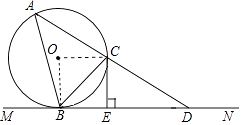
∵MN是⊙O的切线,
∴OB⊥MN,
∴∠OBE=90°,
∵CE⊥MN,
∴∠CEB=90°,
∵∠BOC=2∠BAC=2×45°=90°,
∴四边形OBEC为矩形,
∴∠OCE=90°,
∴OC⊥CE,
∴CE是⊙O的切线
(2)解:∵OB=OC,
∴四边形OBEC为正方形,
∴BE=CE=OB=r,
∴DE=BD﹣BE=4﹣r,
在Rt△CED中,∵tanD= ![]() =tan30°,
=tan30°,
∴ ![]() =
= ![]() ,
,
∴r=2 ![]() ﹣2
﹣2
【解析】(1)连接OC、OB,依据切线的性质可得到∠OBE=90°,然后,再由圆周角定理得到∠BOC=2∠BAC=90°,接下来,再证明四边形OBEC为矩形,根据矩形的性质可得到∠OCE=90°,最后,根据切线的判定定理进行判断即可;
(2)先证明四边形OBEC为正方形,然后再依据正方形的性质得到BE=CE=OB=r,然后在Rt△CED中利用正切的定义得到![]() =
=![]() ,然后再解关于r的方程即可.
,然后再解关于r的方程即可.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
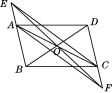
【题目】如图,在ABCD中,点O是AC与BD的交点,过点O的直线与BA的延长线,DC的延长线分别交于点E,F.
(1)求证:△AOE≌△COF.
(2)连接EC,AF,则EF与AC满足什么数量关系时,四边形AECF是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场经营的某品牌童装,4月的销售额为20000元,为扩大销量,5月份商场对这种童装打9折销售,结果销量增加了50件,销售额增加了7000元.
(1)求该童装4月份的销售单价;
(2)若4月份销售这种童装获利8000元,6月全月商场进行“六一”儿童节促销活动.童装在4月售价的基础上一律打8折销售,若该童装的成本不变,则销量至少为多少件,才能保证6月的利润比4月的利润至少增长25%?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】益马高速通车后,将桃江马迹塘的农产品运往益阳的运输成本大大降低。马迹塘一农户需要将A,B两种农产品定期运往益阳某加工厂,每次运输A,B产品的件数不变,原来每运一次的运费是1200元,现在每运一次的运费比原来减少了300元,A,B两种产品原来的运费和现在的运费(单位:元∕件)如下表所示:
品种 | A | B |
原来的运费 | 45 | 25 |
现在的运费 | 30 | 20 |
(1)求每次运输的农产品中A,B产品各有多少件?
(2)由于该农户诚实守信,产品质量好,加工厂决定提高该农户的供货量,每次运送的总件数增加8件,但总件数中B产品的件数不得超过A产品件数的2倍,问产品件数增加后,每次运费最少需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣ ![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.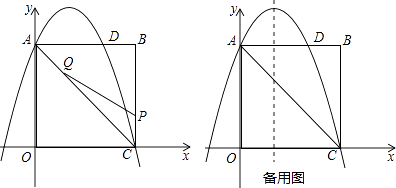
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣ ![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=16°31′,则飞机A与指挥台B的距离等于(结果保留整数)(参考数据sin16°31′=0.28,cos16°31′=0.95,tan16°31′=0.30)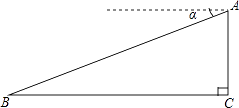
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以A(2,0),B(0,t)为顶点作等腰直角△ABC(其中∠ABC=90°,且点C落在第一象限内),则点C关于y轴的对称点C’的坐标为___.(用t的代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com