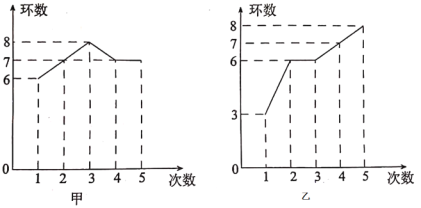
[题目]甲.乙两人在相同的条件下各射靶5次.每次射靶的成绩情况如图所示:(1)请你根据图中的数据填写下表:姓名平均数众数甲7乙6(2)请通过计算方差.说明谁的成绩更稳定．题目和参考答案——青夏教育精英家教网—

【题目】甲、乙两人在相同的条件下各射靶5次，每次射靶的成绩情况如图所示：

（1）请你根据图中的数据填写下表：

姓名	平均数	众数
甲		7
乙	6

（2）请通过计算方差，说明谁的成绩更稳定．

【答案】（1）7；6；（2）甲比乙更稳定

【解析】

（1）根据众数的定义和平均数公式计算即可得出答案；
（2）根据方差的公式分别计算并结合方差的意义分析得出答案即可．

解：（1）甲的平均数= ，乙的射靶的成绩中，6环出现次数最多为2次，故其众数为6；

完成表格如下：

姓名	平均数	众数
甲	7	7
乙	6	6

（2）S甲2=[ 6 7）2 （7 7）2 （8 7）2（7 7）2 （77）2]=；

S乙2=[ 3 6）2 （6 6）2 （6 6）2（7 6）2 （8 6）2 =

因为S甲2＜S乙2，所以甲比乙更稳定

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图11，一转盘被等分成三个扇形，上面分别标有关－1，1，

2中的一个数，指针位置固定，转动转盘后任其自由停止，这时，鞭个扇形恰好停在指针所

指的位置，并相应得到这个扇形上的数（若指针恰好指在等分线上，当做指向右边的扇形）.

⑴若小静转动转盘一次，求得到负数的概率；

⑵小宇和小静分别转动一次，若两人得到的数相同，则称两人“不谋而合”，用列表法（或画树形图）求两人“不谋而合”的概率.

查看答案和解析>>

科目：初中数学 来源： 题型：

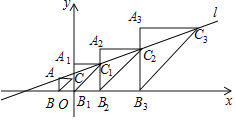
【题目】如图，在平面直角坐标系中，ABC，A1B1C1，A2B2C2，A3B3C3…AnBnCn都是等腰直角三角形，点B，B1，B2，B3…Bn都在x轴上，点B1与原点重合，点A，C1，C2，C3…Cn都在直线l：y＝x+上，点C在y轴上，AB∥A1B1∥A2B2∥…∥AnBn∥y轴，AC∥A1C1∥A2C2∥…∥AnCn∥x轴，若点A的横坐标为﹣1，则点Cn的纵坐标是_____．

查看答案和解析>>

科目：初中数学 来源： 题型：

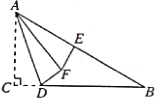
【题目】如图，已知在△ABC中，，，，点E为AB的中点，D为BC边上的一动点，把△ACD沿AD折叠，点C落在点F处，当△AEF为直角三角形时，CD的长为__________．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，等边三角形ABC和正方形DEFG按如图所示摆放，其中 D，E两点分别在AB，BC上，且BD=DE．若AB=12，DE=4，则△EFC的面积为（）

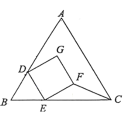
A.4B.8C.12D.16

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，∠B=30°，∠C=45°，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E。若DE=1，则BC的长为（）

A.2+B.C.D.3

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（问题提出）：有同样大小正方形256个，拼成如图1所示的的一个大的正方形．请问如果用一条直线穿过这个大正方形的话，最多可以穿过多少个小正方形？

（问题探究）：我们先考虑以下简单的情况：一条直线穿越一个正方形的情况．（如图2）

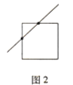
从图中我们可以看出，当一条直线穿过一个小正方形时，这条直线最多与正方形上、下、左、右四条边中的两个边相交，所以当一条直线穿过一个小正方形时，这条直线会与其中某两条边产生两个交点，并且以两个交点为顶点的线段会全部落在小正方形内．

这就启发我们：为了求出直线最多穿过多少个小正方形，我们可以转而去考虑当直线穿越由小正方形拼成的大正方形时最多会产生多少个交点.然后由交点数去确定有多少根小线段，进而通过线段的根数确定下正方形的个数．

再让我们来考虑正方形的情况（如图3）：

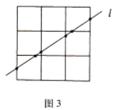
为了让直线穿越更多的小正方形，我们不妨假设直线右上方至左下方穿过一个的正方形，我们从两个方向来分析直线穿过正方形的情况：从上下来看，这条直线由下至上最多可穿过上下平行的两条线段；从左右来看，这条直线最多可穿过左右平行的四条线段；这样直线最多可穿过的大正方形中的六条线段，从而直线上会产生6个交点，这6个交点之间的5条线段，每条会落在一个不同的正方形内，因此直线最多能经过5个小正方形．

（问题解决）：

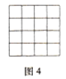
（1）有同样大小的小正方形16个，拼成如图4所示的的一个大的正方形．如果用一条直线穿过这个大正方形的话，最多可以穿过_________个小正方形．

（2）有同样大小的小正方形256个，拼成的一个大的正方形.如果用一条直线穿过这个大正方形的话，最多可以穿过___________个小正方形．

（3）如果用一条直线穿过的大正方形的话，最多可以穿过___________个小正方形．

（问题拓展）：

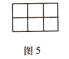
（4）如果用一条直线穿过的大长方形的话（如图5），最多可以穿过个___________小正方形．

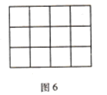
（5）如果用一条直线穿过的大长方形的话（如图6），最多可以穿过___________个小正方形．

（6）如果用一条直线穿过的大长方形的话，最多可以穿过________个小正方形．

（类比探究）：

由二维的平面我们可以联想到三维的立体空间，平面中的正方形中四条边可联想到正方体中的正方形的六个面，类比上面问题解决的方法解决如下问题：

（7）如图7有同样大小的小正方体8个，拼成如图所示的的一个大的正方体.如果用一条直线穿过这个大正方体的话，最多可以穿过___________个小正方体．

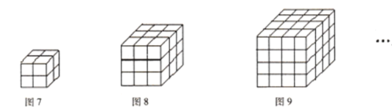
（8）如果用一条直线穿过的大正方体的话，最多可以穿过_________个小正方体．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】九年级某班准备选拔四名男生参加学校运动会接力比赛，进行了一次50米短跑测验，成绩如下，(单位：秒)6.9 7.0 7.1　7.2　7.0　7.4　7.3　7.5　7.0　7.4 7.3 6.8 7.0　7.1 7.3 6.9 7.1 7.2 7.4 6.9 7.0 7.2 7.0 7.2 7.6

班主任老师按0.2秒的组距分段，统计每个成绩段出现的频数，填入频数分布表，并绘制了频数分布直方图．